Question

Find the equation of the right bisector plane of the segment joining (2, 3, 4) and (6, 7, 8)

Answer 1

Hint : A right bisector is a line that cuts another line at midpoint at 90 degrees. It is more often called a perpendicular bisector. To solve this we need to know the formula for Cartesian equation of a line passes through two points $({x_1},{y_1},{z_1})$ and $({x_{2,}}{y_2},{z_2})$ . Also remember the basic definition of direction cosines of a line.

Complete step-by-step answer :
If we describe the given problem in diagram, we get

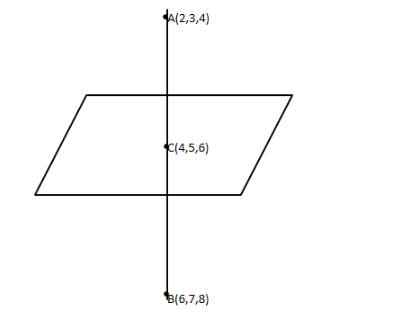
We know the Cartesian equation of a line passes through two points $({x_1},{y_1},{z_1})$ and $({x_{2,}}{y_2},{z_2})$ is:

\dfrac{{x - {x_1}}}{{{x_2} - {x_1}}} = \dfrac{{y - {y_1}}}{{{y_2} - {y_1}}} = \dfrac{{z - {z_1}}}{{{z_2} - {z_1}}} \ \ \ \ \end{gathered} $$ . Here, $$({x_1},{y_1},{z_1}) $$ = (2, 3, 4) and $$({x_{2,}}{y_2},{z_2}) $$ = (6, 7, 8) Substituting this in above, $$ \Rightarrow \dfrac{{x - 2}}{{6 - 2}} = \dfrac{{y - 3}}{{7 - 3}} = \dfrac{{z - 4}}{{8 - 4}} $$ $$ \Rightarrow \dfrac{{x - 2}}{4} = \dfrac{{y - 3}}{4} = \dfrac{{z - 4}}{4} $$ . Which is equivalent to $$ \begin{gathered} \Rightarrow \dfrac{{x - 2}}{1} = \dfrac{{y - 3}}{1} = \dfrac{{z - 4}}{1} \ \ \ \ \end{gathered} $$ Therefore direction cosines are (1, 1, 1). The bisector point is given C is given by, $$ \Rightarrow \left( { \dfrac{{{x_1} + {x_2}}}{2}, \dfrac{{{y_1} + {y_2}}}{2}, \dfrac{{{z_1} + {z_2}}}{2}} \right) $$ Substituting $$({x_1},{y_1},{z_1}) $$ = (2, 3, 4) and $$({x_{2,}}{y_2},{z_2}) $$ = (6, 7, 8) $$ \Rightarrow \left( { \dfrac{{2 + 6}}{2}, \dfrac{{3 + 7}}{2}, \dfrac{{4 + 8}}{2}} \right) $$ $$ \Rightarrow (4,5,6) $$ We get the point C (4, 5, 6). Hence the equation of the right bisector in a plane is $$l(x - {c_1}) + m(y - {c_2}) + n(z - {c_3}) = 0 $$ . Where, $$(l,m,n) $$ are direction cosines and $$({c_1},{c_2},{c_3}) = (4,5,6) $$ . Substituting above we get, $$1(x - 4) + 1(y - 5) + 1(z - 6) = 0 $$ Keeping the variable on one side and constant on the other side, $$ \Rightarrow x + y + z = 4 + 5 + 6 $$ $$ \Rightarrow x + y + z = 15 $$ Hence, the equation of the right bisector plane of the segment joining (2, 3, 4) and (6, 7, 8) is $$x + y + z = 15 $$ **So, the correct answer is “ $$x + y + z = 15 $$ ”.** **Note** : In this type of question we need to remember the Cartesian equation of a line passes through two points $$({x_1},{y_1},{z_1}) $$ and $$({x_{2,}}{y_2},{z_2}) $$ . Direction cosines of a line are the cosines of the angles made by the line with the positive directions of the coordinate axes. Also remember the equation of the bisector in a plane. Which is the same for any problem, so that you can solve for different points.