Question

Find the equation of the plane that cuts the co-ordinate axis at $\left( a,0,0 \right)$, $\left( 0,b,0 \right)$ and $\left( 0,0,c \right)$.

Answer 1

We solve this question by first considering the given points as $A\left( a,0,0 \right)$, $B\left( 0,b,0 \right)$ and $C\left( 0,0,c \right)$. Then we Find the direction ratios of line AB and line AC. Then we use the property, the line perpendicular to the lines $\overrightarrow{a}$ and $\overrightarrow{b}$ is $\left( \overrightarrow{a}\times \overrightarrow{b} \right)$. Using this we find the direction ratios of the line that is normal to AB and AC. Then we acknowledge that as those lines are on plane their normal is a normal to the plane. Then we use the formula, equation of the plane passing through the point $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and with direction ratios $\left( a,b,c \right)$ is $a\left( x-{{x}_{1}} \right)+b\left( y-{{y}_{1}} \right)+c\left( z-{{z}_{1}} \right)=0$. Then substituting the direction ratios and any one of the points we can find the equation of the plane.

Complete step-by-step solution
We are given that a plane cuts the co-ordinate axis at points $\left( a,0,0 \right)$, $\left( 0,b,0 \right)$ and $\left( 0,0,c \right)$.
Let us say those points are represented as $A\left( a,0,0 \right)$, $B\left( 0,b,0 \right)$ and $C\left( 0,0,c \right)$.

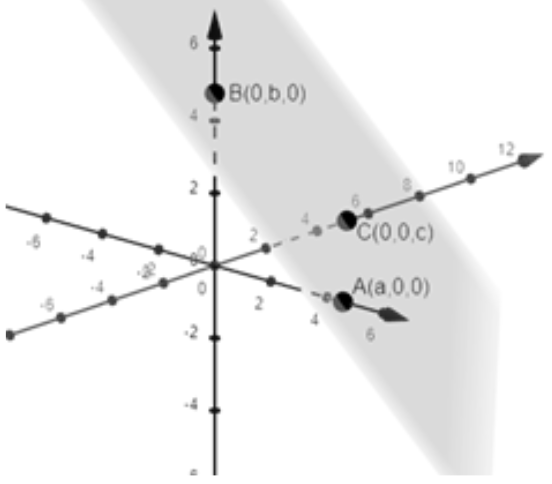
As, A, B, and C are points on the plane, lines AB and AC are also on the plane. So, if a normal is drawn to the lines both AB and AC then it is also normal to the plane.
So, direction ratios of the normal to AB and AC are the direction ratios of the given plane.
So, now let us find the direction ratios of line AB.
So, direction ratios of AB are

& \Rightarrow \left( 0-a,b-0,0-0 \right) \\\ & \Rightarrow \left( -a,b,0 \right) \\\ \end{aligned}$$ Now let us find the direction ratios of line AC. So, direction ratios of AC are $$\begin{aligned} & \Rightarrow \left( 0-a,0-0,c-0 \right) \\\ & \Rightarrow \left( -a,0,c \right) \\\ \end{aligned}$$ Now let us find the direction ratios of the line perpendicular to AB and AC. Now let us consider the property, the line perpendicular to the lines $\overrightarrow{a}$ and $\overrightarrow{b}$ is $\left( \overrightarrow{a}\times \overrightarrow{b} \right)$. So, using this we get that the direction ratios of normal to lines AB and AC are $\left( AB\times AC \right)$. $\begin{aligned} & \Rightarrow AB\times AC=\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\\ -a & b & 0 \\\ -a & 0 & c \\\ \end{matrix} \right| \\\ & \Rightarrow AB\times AC=\left| \begin{matrix} b & 0 \\\ 0 & c \\\ \end{matrix} \right|\hat{i}-\left| \begin{matrix} -a & 0 \\\ -a & c \\\ \end{matrix} \right|\hat{j}+\left| \begin{matrix} -a & b \\\ -a & 0 \\\ \end{matrix} \right|\hat{k} \\\ & \Rightarrow AB\times AC=\left( bc-0 \right)\hat{i}-\left( -ac-0 \right)\hat{j}+\left( 0-\left( -ab \right) \right)\hat{k} \\\ & \Rightarrow AB\times AC=bc\hat{i}+ac\hat{j}+ab\hat{k} \\\ \end{aligned}$ So, we get the direction ratios of normal to AB and AC, thereby the direction ratios of the normal to the plane are $\left( bc,ac,ab \right)$. Now let us consider the formula for equation of the plane passing through the point $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and with direction ratios $\left( a,b,c \right)$ is $a\left( x-{{x}_{1}} \right)+b\left( y-{{y}_{1}} \right)+c\left( z-{{z}_{1}} \right)=0$ So, the equation of the plane through point $\left( a,0,0 \right)$ and with direction ratios $\left( bc,ac,ab \right)$ is $\begin{aligned} & \Rightarrow bc\left( x-a \right)+ac\left( y-0 \right)+ab\left( z-0 \right)=0 \\\ & \Rightarrow bcx-abc+acy+abz=0 \\\ & \Rightarrow bcx+acy+abz=abc \\\ & \Rightarrow \dfrac{bcx}{abc}+\dfrac{acy}{abc}+\dfrac{abz}{abc}=1 \\\ & \Rightarrow \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1 \\\ \end{aligned}$ So, equation of the plane that cuts the co-ordinate axis at $\left( a,0,0 \right)$, $\left( 0,b,0 \right)$ and $\left( 0,0,c \right)$ is $\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$. **Hence answer is $\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$.** **Note:** We can also solve this question by directly using the formula, equation of the plane that cuts co-ordinate axis at $\left( l,0,0 \right)$, $\left( 0,m,0 \right)$ and $\left( 0,0,n \right)$ is $\dfrac{x}{l}+\dfrac{y}{m}+\dfrac{z}{n}=1$ Using this formula, we get the equation of the plane as $\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$. Hence answer is $\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$.