Question

Find the equation of the parabola which is symmetric about the y-axis and passes through the point (3, -9).

Answer 1

Hint : We solve this by finding where the points (3, -9) lie in the equation of parabola. Since the parabola is symmetric about the y-axis is ${x^2} = 4ay$ or ${x^2} = - 4ay$ . By using the given points (3, -9) we can find the value of ‘a’ and substituting in the required equation we will get the equation of parabola.

Complete step-by-step answer :
We know the equation of parabola about the y-axis is ${x^2} = 4ay$ or ${x^2} = - 4ay$ .
Since the points (3, -9) lie in the fourth quadrant so the equation of parabola about the y-axis is ${x^2} = - 4ay$ . See the below diagram you will understand easily.

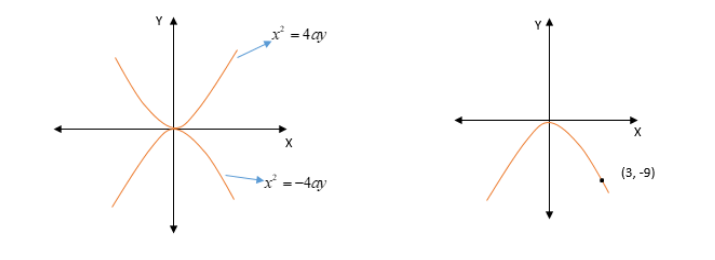
Hence, the equation of parabola is ${x^2} = - 4ay$ . ---- (1)
We need to find the value of ‘a’.
Now parabola passes through (3, -9), put $x = 3$ and $y = - 9$ in equation (1). We get:
$\Rightarrow {3^2} = - 4 \times a \times ( - 9)$
$\Rightarrow 9 = - 4 \times a \times ( - 9)$
We know the product of negative and negative is positive and rearranging the above equation we get:
$\Rightarrow a = \dfrac{9}{{9 \times 4}}$
$\Rightarrow a = \dfrac{1}{4}$
We know the value of ‘a’. Now substituting in the equation (1). We get
$\Rightarrow {x^2} = - 4\left( {\dfrac{1}{4}} \right)y$
Cancelling 4,
$\Rightarrow {x^2} = - y$
$\Rightarrow {x^2} + y = 0$ Is the required equation.
The equation of the parabola which is symmetric about the y-axis and passes through the point (3, -9) is ${x^2} + y = 0$ .
So, the correct answer is “ ${x^2} + y = 0$ ”.

Note : If they ask the same question with the same points with a symmetric about the x-axis then we have the equation of parabola is ${y^2} = 4ax$ or ${y^2} = - 4ax$ . Follow the same procedure as above you will get the equation of parabola. Careful about the points where it lies (quadrant). Remember the equations of parabola about x-axis and y-axis.