Solveeit Logo
Login

Question

Question: Find the equation of the normal to the hyperbola \({{x}^{2}}-4{{y}^{2}}=36\) at the point (10, 4)....

Find the equation of the normal to the hyperbola x2−4y2=36{{x}^{2}}-4{{y}^{2}}=36 at the point (10, 4).

Explanation

Solution

Hint: We know that the product of the slopes of a given curve and the normal/tangent to that curve at a given point always equals to ‘-1’. The slope of a curve can be found by applying differentiation on the equation. The normal is a straight line and we can use the calculated slope to find its equation.

Complete step-by-step answer:

In order to find the equation of the normal to the given hyperbola we firstly need to find the slope of the hyperbola which can be found by taking the derivative with respect to ‘x’ on both sides of the hyperbola equation.
So,
d(x2)dx−d(4y2)dx=d(36)dx\dfrac{d\left( {{x}^{2}} \right)}{dx}-\dfrac{d\left( 4{{y}^{2}} \right)}{dx}=\dfrac{d\left( 36 \right)}{dx}

Now we know, d(xn)dx=n(xn−1)\dfrac{d\left( {{x}^{n}} \right)}{dx}=n\left( {{x}^{n-1}} \right) , so the above equation becomes
⇒2x−4d(y2)dx=0 ⇒2x−8ydydx=0 ⇒dydx=−2x−8y ⇒dydx=x4y.............(i) \begin{aligned} & \Rightarrow 2x-\dfrac{4d\left( {{y}^{2}} \right)}{dx}=0 \\\ & \Rightarrow 2x-8y\dfrac{dy}{dx}=0 \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{-2x}{-8y} \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{x}{4y}.............(i) \\\ \end{aligned}

As we know the product of slopes of the curve and its normal is always -1. Therefore, the slope of normal will be −dxdy-\dfrac{dx}{dy} .

That means, from equation (i) we can substitute,
−dxdy=−4yx-\dfrac{dx}{dy}=-\dfrac{4y}{x}

Now the slope of normal at point (10,4)\left( 10,4 \right) will be,
−dxdy=−4(4)(10) −dxdy=−1610=−85..............(ii) \begin{aligned} & -\dfrac{dx}{dy}=-\dfrac{4(4)}{(10)} \\\ & -\dfrac{dx}{dy}=-\dfrac{16}{10}=-\dfrac{8}{5}..............(ii) \\\ \end{aligned}

The equation of the normal can be written from the equation of the line,
y−y1=m(x−x1)y-{{y}_{1}}=m(x-{{x}_{1}})
Here, x1=10,y1=4,m=−85{{x}_{1}}=10,{{y}_{1}}=4,m=-\dfrac{8}{5}

Substituting the values in equation of line, we get
y−4=−85(x−10)y-4=-\dfrac{8}{5}\left( x-10 \right)

On cross-multiplying, we get
⇒5(y−4)=−8(x−10) ⇒5y−20=−8x+80 ⇒8x+5y=80+20 \begin{aligned} & \Rightarrow 5\left( y-4 \right)=-8\left( x-10 \right) \\\ & \Rightarrow 5y-20=-8x+80 \\\ & \Rightarrow 8x+5y=80+20 \\\ \end{aligned}
⇒8x+5y=100\Rightarrow 8x+5y=100

The equation of the normal to the given hyperbola is 8x+5y=1008x+5y=100.

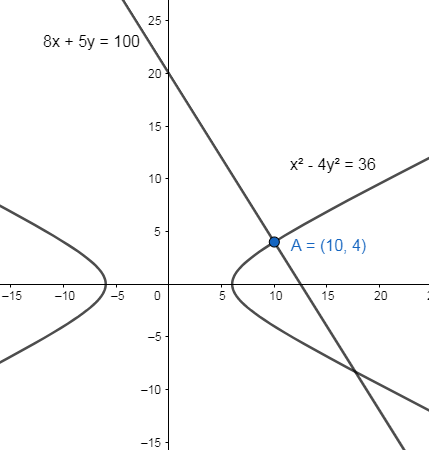
Note: The caution must be taken when writing the product of slopes. Generally students make mistakes by taking the product of slopes of the curve and it’s normal as ‘1’ instead of ‘-1’. In this case we get the wrong answer.