Question

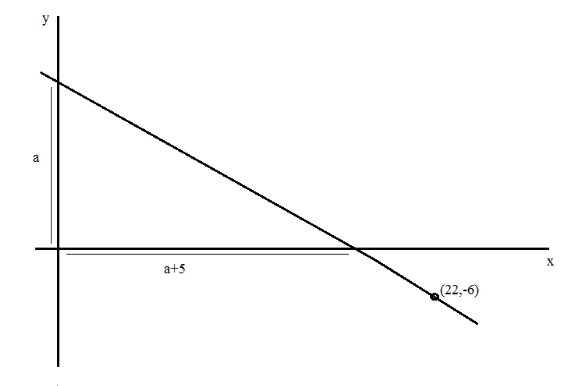
Find the equation of the lines which passes through the point (22,-6) and whose intercept on the x-axis exceeds the intercept on the y-axis by 5.

Answer 1

Hint : In this question, we need to determine the equation of the line(s) which passes through the point (22,-6) and whose intercept on the x-axis exceeds the intercept on the y-axis by 5. For this, we will follow the relation between the x and the y-axes of the equation of the line and satisfy the given conditions simultaneously.

Complete step-by-step answer :
Let the intercept made by the line on the y-axis be ‘a’.
According to the question, the intercept made by the line on the x-axis is 5 more than the intercept made by the line of the y-axis. So,
The X-intercept of the line is given by ‘a+5’.

Following the standard equation of the line $\dfrac{x}{a} + \dfrac{y}{b} = 1$ where ‘a’ and ‘b’ are the intercepts on the x and the y-axes respectively by the line, and x and y are the variables which satisfy the equation of the line.
Here, the x and the y-intercepts are ‘a+5’ and ‘a’ so, substituting these values in the equation $\dfrac{x}{a} + \dfrac{y}{b} = 1$ to determine the equation of the line in terms of ‘a’.
$\Rightarrow \dfrac{x}{a} + \dfrac{y}{b} = 1 \\\ \Rightarrow \dfrac{x}{{a + 5}} + \dfrac{y}{a} = 1 \\\ \Rightarrow ax + (a + 5)y = a(a + 5) - - - - (i) \;$
Also, it is given that the line is passing through the point (22,-6) so, substituting the values of x and y in the equation (i) to determine the value of ‘a’.
$\Rightarrow ax + (a + 5)y = a(a + 5) \\\ \Rightarrow 22a + (a + 5)( - 6) = a(a + 5) \\\ \Rightarrow 22a - 6a - 30 = {a^2} + 5a \\\ \Rightarrow {a^2} + 5a + 6a - 22a + 30 = 0 \\\ \Rightarrow {a^2} - 11a + 30 = 0 - - - - (ii) \;$
Solving the equation (ii) by following the splitting the middle term for the values of ‘a’:
$\Rightarrow {a^2} - 11a + 30 = 0 \\\ \Rightarrow {a^2} - 6a - 5a + 30 = 0 \\\ \Rightarrow a(a - 6) - 5(a - 6) = 0 \\\ \Rightarrow (a - 5)(a - 6) = 0 \\\ a = 5;6 \;$
Here we got two different values of ‘a’ so two equations of the lines are possible with the given conditions.
Case 1. a=5
For the y-intercept as 5, the x-intercept is given as $a + 5 = 5 + 5 = 10$. So, the equation of the line is given as:
$\Rightarrow \dfrac{x}{{10}} + \dfrac{y}{5} = 1 \\\ \Rightarrow x + 2y = 10 \\\ \Rightarrow x + 2y - 10 = 0 \\\$
Case 2. a=6
For the y-intercept as 6, the x-intercept is given as $a + 5 = 6 + 5 = 11$. So, the equation of the line is given as:
$\Rightarrow \dfrac{x}{{11}} + \dfrac{y}{6} = 1 \\\ \Rightarrow 6x + 11y = 66 \\\ \Rightarrow x + 2y - 66 = 0 \\\$
Hence, the equations of the lines which passes through the point (22,-6) and whose intercept on the x-axis exceeds the intercept on the y-axis by 5 are $x + 2y - 10 = 0$ and $x + 2y - 66 = 0$.
So, the correct answer is “$x + 2y - 10 = 0$ and $x + 2y - 66 = 0$.”.

Note : Students must be very careful while substituting the values of the x and the y-intercepts in the equation of the line while satisfying the given conditions simultaneously. Moreover, when a point lies on the line, then, it satisfies the equation of the line.