Question

Find the equation of the line(s) passing through the point $\left( { - 3,5} \right)$ among the following options:
(A) $x = - 3$
(B) $y = - 3$
(C) $x = 5$
(D) $y = 5$

Answer 1

Try making a diagram of the Cartesian plane and mark the point given in the question. Use the concept of the equation of line parallel to x-axis and y-axis. Find out the point of intersection of the lines with x and y-axis to find the correct equations from the given options.

Complete step-by-step answer:

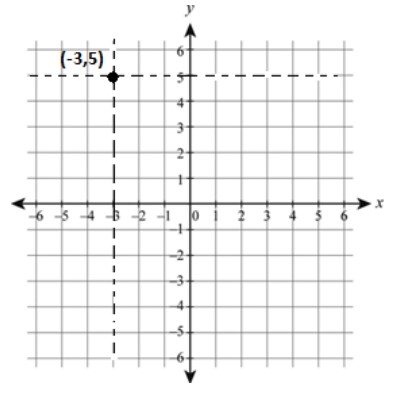
Let’s try to understand the question first. We are given one point $\left( { - 3,5} \right)$ and four options with the equation of the line. The solution is to find the equation that passes through the point$\left( { - 3,5} \right)$.
Since it is well known and reasonable that there can be the infinite number of the line that can pass through a single given point. So, we should try to solve this problem through reasoning.
Draw a rough figure of a Cartesian plane and mark point $\left( { - 3,5} \right)$on it. Look into the figure as we go to further steps.
Firstly, you should understand that the equation of x-axis is $y = 0$ and equation of y-axis is $x = 0$.
Secondly, the equation of any line parallel to the x-axis is $y = a$ for all integers $'a'$ and the equation of any line parallel to y-axis is $x = a$ for all integers$'a'$. Also, a line $y = a$ is parallel to the x-axis and passes to the point $\left( {0,a} \right)$ at the y-axis. Similarly, a line $x = a$ is parallel to the y-axis and passes to the point $\left( {a,0} \right)$ at x-axis.
Therefore, for any point $\left( { - 3,5} \right)$, if a line passing to it and is parallel to the x-axis, will always pass the y-axis at the point $\left( {0,5} \right)$. And any line passing to $\left( { - 3,5} \right)$ is parallel to the y-axis, and will always pass the x-axis at a point $\left( { - 3,0} \right)$.
Thus, the equation for such lines will be $y = 5$ and $x = - 3$. Any other line parallel to either x-axis or y-axis will never pass through the point $\left( { - 3,5} \right)$.

So, the correct answer is “Option A and D”.

Note: Make a rough diagram while solving such problems to make it more understandable. You can also check for the rest of the options given in the question. The Option (B) $y = - 3$ will pass through $(0, - 3)$ parallel to x-axis and Option (C) $x = 5$ will pass through $\left( {5,0} \right)$ parallel to the y-axis.