Question

Find the equation of the line midway between the parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0
A) $2x + 3y + \dfrac{5}{7} = 0$
B) $3x + 2y + \dfrac{{11}}{6} = 0$
C) $5x + 7y + \dfrac{9}{{11}} = 0$
D) None of these

Answer 1

Hint : As both the given lines are parallel, the line in the midway will also be parallel to both. We can use the following properties of parallel lines:
i) Coefficient of x and y in both the lines are same and only the constants are different
ii) Distance between two parallel lines can be given as:
$d = \left| {\dfrac{{{c_2} - {c_1}}}{{\sqrt {{a^2} + {b^2}} }}} \right|$ where,
${c_1}$ and ${c_2}$ are the constants of respective lines
a and b are the coefficients of x and y (same for both the lines.
General equation of a line can be given as:
ax + by + c = 0

** Complete step-by-step answer** :

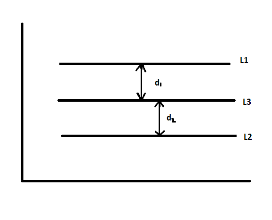
If the lines are parallel, the value of their coefficients of x and y are the same but the constant is different.
Given equation of lines
Line 1 (L1) = 9x + 2y – 7 = 0
In simplified form, it can be written as:
$3x + 2y - \dfrac{7}{3}$ (Taking 3 common)
Line 2 (L2) = 3x + 2y + 6 = 0
We can see that the coefficients of x and y are same in both the equations but the constants are different.
Comparing with general equation of line:
a = 3 and b = 2
Let the equation of the required mid-way line be:
ax + by + c, substituting the values:
Line (L3) = 3x + 2y + c ___________ (1)
As the line mid-way (in the middle) of two parallel lines will also be parallel to both.
Now, the distance between L1 and L3$\left( {{d_1}} \right)$ = distance between L2 and L3 $\left( {{d_2}} \right)$
${d_1} = {d_2}$ ________ (2)
(As L3 is in the middle)
$d = \left| {\dfrac{{{c_2} - {c_1}}}{{\sqrt {{a^2} + {b^2}} }}} \right|$ __________ (3)
Distance between L1 and L3:
${c_2} = c \\\ {c_1} = \left( { - \dfrac{7}{3}} \right) \\\$
a = 3
b = 2
Substituting these values in (3), we get:
${d_1} = \left| {\dfrac{{c - \left( { - \dfrac{7}{3}} \right)}}{{\sqrt {{{(3)}^2} + {{(2)}^2}} }}} \right|$
Distance between L2 and L3:

$${c_2} = c \\\ {c_1} = 6 \\\$$

a = 3
b = 2
Substituting these values in (3), we get:
${d_2} = \left| {\dfrac{{c - 6}}{{\sqrt {{{(3)}^2} + {{(2)}^2}} }}} \right|$
From (2):
${d_1} = {d_2}$
Substituting the values, we get:
$\left| {\dfrac{{c - \left( { - \dfrac{7}{3}} \right)}}{{\sqrt {{{(3)}^2} + {{(2)}^2}} }}} \right| = \left| {\dfrac{{c - 6}}{{\sqrt {{{(3)}^2} + {{(2)}^2}} }}} \right|$
As the denominators are equal on both RHS and LHS, they get cancelled
$\left| {c + \dfrac{7}{3}} \right| = \left| {c - 6} \right| \\\ c + \dfrac{7}{3} = - c + 6 \\\ c + c = 6 - \dfrac{7}{3} \\\ 2c = \dfrac{{11}}{3} \\\ c = \dfrac{{11}}{6} \\\$
Substituting this value of c in (1), we get:
Line (L3) = 3x + 2y + c
= $3x{\text{ }} + {\text{ }}2y{\text{ }} + {\text{ }}\dfrac{{11}}{6}$
Therefore, equation of the line midway between the parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0 is $3x{\text{ }} + {\text{ }}2y{\text{ }} + {\text{ }}\dfrac{{11}}{6}$.
So, the correct answer is “Option B”.

Note : The line in the middle of the two lines will always be equidistant to both and hence the distance of the middle line with first will be equal to that with the second.
Parallel lines that are far extended can never intersect.
In general, it can be said that the parallel lines are equidistant and point in the same direction