Solveeit Logo
Login

Question

Question: Find the equation of the line in vector form which passes through \[\left( {1,2,3} \right)\] and par...

Find the equation of the line in vector form which passes through (1,2,3)\left( {1,2,3} \right) and parallel to the vector 3i^+2j^−2k^3\widehat i + 2\widehat j - 2\widehat k.

Explanation

Solution

Hint : Here in this question, we have to find the vector equation of a line passing through a point with position vector a→\overrightarrow a and parallel to a vector b→\overrightarrow b using a equation r→=a→+λb→\overrightarrow r = \overrightarrow a + \lambda \overrightarrow b , where a→\overrightarrow a is the line passes through (1,2,3)\left( {1,2,3} \right) so a→=1i^+2j^+3k^\overrightarrow a = 1\widehat i + 2\widehat j + 3\widehat k and b→=3i^+2j^−2k^\overrightarrow b = 3\widehat i + 2\widehat j - 2\widehat k , on substituting we get the required solution.

Complete step-by-step answer :
Let a→\overrightarrow a be the position vector of the given point A with respect to the origin O of the rectangular coordinate system. Let ll be the line which passes through the point A and is parallel to a given vector b→\overrightarrow b . Let r→\overrightarrow r be the position vector of an arbitrary point P on the line.

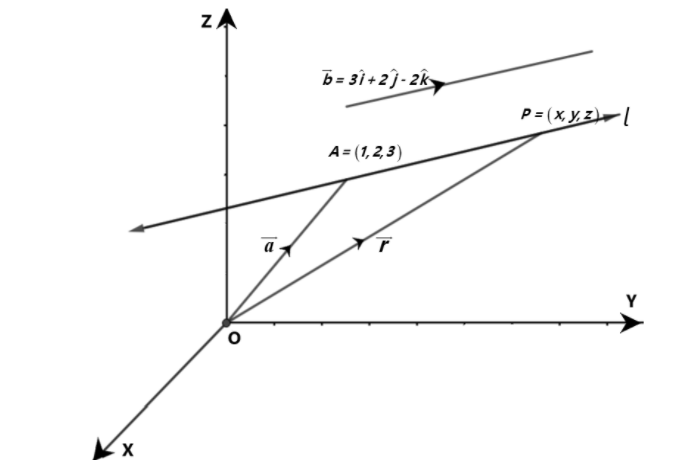
Here, AP→\overrightarrow {AP} is parallel to the vector b→\overrightarrow b , i.e., AP→=λb→\overrightarrow {AP} = \lambda \overrightarrow b , where λ\lambda is some real number.
But
AP→=OP→−OA→\overrightarrow {AP} = \overrightarrow {OP} - \overrightarrow {OA}
λb→=r→−a→\lambda \overrightarrow b = \overrightarrow r - \overrightarrow a
Hence, the vector equation of the line is given by r→=a→+λb→\overrightarrow r = \overrightarrow a + \lambda \overrightarrow b -----(1)
Given, the line passes through (1,2,3)\left( {1,2,3} \right), so the position vector a→=1i^+2j^+3k^\overrightarrow a = 1\widehat i + 2\widehat j + 3\widehat k and parallel to the vector 3i^+2j^−2k^3\widehat i + 2\widehat j - 2\widehat k.
Now, putting value of a→\overrightarrow a and b→\overrightarrow b in equation (1), we have
∴   r→=(1i^+2j^+3k^)+λ(3i^+2j^−2k^)\therefore \,\,\,\overrightarrow r = \left( {1\widehat i + 2\widehat j + 3\widehat k} \right) + \lambda \left( {3\widehat i + 2\widehat j - 2\widehat k} \right)
Hence, the above equation is a vector equation of line which passes through (1,2,3)\left( {1,2,3} \right) and parallel to the vector 3i^+2j^−2k^3\widehat i + 2\widehat j - 2\widehat k.
So, the correct answer is “Option B”.

Note : Remember, the above solved equation is in vector form and one more form of equation i.e., cartesian form of a line passing through the point (x1,y1,z1)\left( {{x_1},{y_1},{z_1}} \right) and parallel to the vector ai^+bj^+ck^a\widehat i + b\widehat j + c\widehat k is given as x−x1a=y−y1b=z−z1c\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}.
The cartesian form of equation of given question is
Where, (x1,y1,z1)=(1,2,3)\left( {{x_1},{y_1},{z_1}} \right) = \left( {1,2,3} \right) and ai^+bj^+ck^=3i^+2j^−2k^a\widehat i + b\widehat j + c\widehat k = 3\widehat i + 2\widehat j - 2\widehat k i.e., a=3, b=2, c=-2
Then by formula we can written the cartesian equation as:
x−13=y−22=z−3−2\dfrac{{x - 1}}{3} = \dfrac{{y - 2}}{2} = \dfrac{{z - 3}}{{ - 2}}.