Question

Find the equation of the ellipse with its center at (4, -1) focused at (1, -1) and given that it passes through (8, 0).

Answer 1

Hint: In this particular type of question use the concept that the center of the ellipse is at midpoint of both the focus of the ellipse and in ellipse we know that ${b^2} = {a^2}\left( {1 - {e^2}} \right)$ and the distance between the focus is 2ae and the general equation of the ellipse having center ${x_1},{y_1}$ is $\dfrac{{{{\left( {x - {x_1}} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - {y_1}} \right)}^2}}}{{{b^2}}} = 1$ so use these concepts to reach the solution of the question.

Complete step-by-step answer:

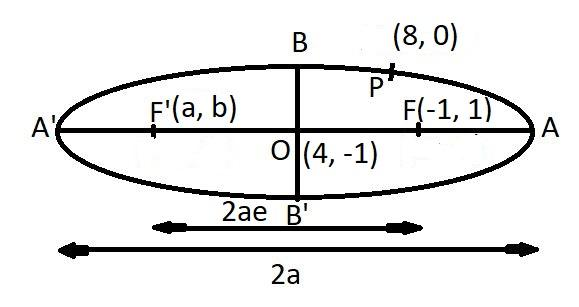
Let O be the center of the ellipse and, F and F’ be the focus of the ellipse respectively as shown in the figure.
Therefore, O = (4, -1) and, F = (1, -1)
As we all know that the center is the midpoint of the F and F’
Let the coordinate of the F’ = (a, b)
Now apply midpoint formula we have,
$\Rightarrow 4 = \dfrac{{1 + a}}{2}, - 1 = \dfrac{{ - 1 + b}}{2}$
Now simplify we have,
$\Rightarrow 8 = 1 + a, - 2 = - 1 + b$
$\Rightarrow a = 7,b = - 1$
So the coordinates of the other focus, F’ = (7, -1)
Now as we see that the y coordinate of the focus F and F’ are same so the major axis of the ellipse is parallel to the x-axis.
Now the general equation of the ellipse with center (${x_1},{y_1}$) is given as,
$\Rightarrow \dfrac{{{{\left( {x - {x_1}} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - {y_1}} \right)}^2}}}{{{b^2}}} = 1$
Now the coordinates of the center is (4, -1) = ${x_1},{y_1}$
So the equation of the ellipse is
$\Rightarrow \dfrac{{{{\left( {x - 4} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y + 1} \right)}^2}}}{{{b^2}}} = 1$............. (1), where (a) and (b) are the length of the semi major axis and semi minor axis respectively.
Now as we know that the distance between the focus = 2ae, where e is the eccentricity.
Now as we know that the distance between two points $\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)$ is given as,
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Let, $\left( {{x_1},{y_1}} \right)$ = (1, -1) and $\left( {{x_2},{y_2}} \right)$ = (7, -1)
Therefore, 2ae = $\sqrt {{{\left( {7 - 1} \right)}^2} + {{\left( { - 1 - \left( { - 1} \right)} \right)}^2}}$
$\Rightarrow 2ae = \sqrt {36 + 0}$
$\Rightarrow 2ae = 6$
$\Rightarrow ae = 3$
Now as we know that in an ellipse
${b^2} = {a^2}\left( {1 - {e^2}} \right)$
$\Rightarrow {b^2} = {a^2} - {\left( 3 \right)^2} = {a^2} - 9$......................... (2)
Now it is given that the ellipse passes from point (8, 0).
So it satisfies the equation of the ellipse so from equation (1) we have,
$\Rightarrow \dfrac{{{{\left( {8 - 4} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {0 + 1} \right)}^2}}}{{{b^2}}} = 1$
$\Rightarrow \dfrac{{16}}{{{a^2}}} + \dfrac{1}{{{b^2}}} = 1$
Now from equation (2) we have,
$\Rightarrow \dfrac{{16}}{{{a^2}}} + \dfrac{1}{{{a^2} - 9}} = 1$
Now simplify this we have,
$\Rightarrow 16\left( {{a^2} - 9} \right) + {a^2} = {a^2}\left( {{a^2} - 9} \right)$
$\Rightarrow 16{a^2} - 144 + {a^2} = {a^4} - 9{a^2}$
$\Rightarrow {a^4} - 26{a^2} + 144 = 0$
Now factorize this we have,
$\Rightarrow {a^4} - 18{a^2} - 8{a^2} + 144 = 0$
$\Rightarrow {a^2}\left( {{a^2} - 18} \right) - 8\left( {{a^2} - 18} \right) = 0$
$\Rightarrow \left( {{a^2} - 18} \right)\left( {{a^2} - 8} \right) = 0$
$\Rightarrow {a^2} = 18,8$
So when, ${a^2} = 18$
From equation (2) we have,
$\Rightarrow {b^2} = 18 - 9 = 9$
And when, ${a^2} = 8$
From equation (2) we have,
$\Rightarrow {b^2} = 8 - 9 = - 1$ (This is not possible it will give us an imaginary value of b)
$\Rightarrow \dfrac{{{{\left( {x - 4} \right)}^2}}}{{18}} + \dfrac{{{{\left( {y + 1} \right)}^2}}}{9} = 1$
So this is the required equation of the ellipse we can also simplify it so we have,
$\Rightarrow \left( {{x^2} + 16 - 8x} \right) + 2\left( {{y^2} + 1 + 2y} \right) = 18$
$\Rightarrow {x^2} + 2{y^2} - 8x + 4y + 18 = 18$
$\Rightarrow {x^2} + 2{y^2} - 8x + 4y = 0$
So this is the required answer.

Note – whenever we face such types of questions the key concept we have to remember is that always recall all the general formulas and the equation of the ellipse which is all stated above and the distance between the two points $\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)$ is given as, $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$.