Question

Find the equation of the directrix of the ellipse $\dfrac{{{x}^{2}}}{100}+\dfrac{{{y}^{2}}}{36}=1$ .

Answer 1

To find the equation of the directrix of the ellipse $\dfrac{{{x}^{2}}}{100}+\dfrac{{{y}^{2}}}{36}=1$ , we will compare this equation to the standard form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and find a and b. Then, we have to find the eccentricity using the formula $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ . We can find the directrix using the formula $x=\pm \dfrac{a}{e}$ . We have to substitute the values and form an equation.

Complete step by step answer:
We have to find the equation of the directrix of the ellipse $\dfrac{{{x}^{2}}}{100}+\dfrac{{{y}^{2}}}{36}=1$ . We know that the standard equation of an ellipse is given by $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ , where where a and b are the length of semi-major and semi-minor axis of an ellipse. Let us compare the given equation to this standard equation. We can see that ${{a}^{2}}=100$ and ${{b}^{2}}=36$ .
Let us consider ${{a}^{2}}=100$ . We have to take the square root of this equation.
$\begin{aligned} & \Rightarrow a=\sqrt{100} \\\ & \Rightarrow a=10\text{ units} \\\ \end{aligned}$
Now, let us consider ${{b}^{2}}=36$ . We have to take the square root of this equation.
$\begin{aligned} & \Rightarrow b=\sqrt{36} \\\ & \Rightarrow b=6\text{ units} \\\ \end{aligned}$
Therefore, we found a and b.
We know that eccentricity of an ellipse is given by
$e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$
Let us substitute the values of a and b in the above equation. We will get the eccentricity of the given ellipse as
$\Rightarrow e=\sqrt{1-\dfrac{36}{100}}$
Let us simplify the RHS.
$\begin{aligned} & \Rightarrow e=\sqrt{\dfrac{100-36}{100}} \\\ & \Rightarrow e=\sqrt{\dfrac{64}{100}} \\\ & \Rightarrow e=\dfrac{\sqrt{64}}{\sqrt{100}} \\\ \end{aligned}$
We know that $\sqrt{64}=8$ and $\sqrt{100}=10$ . Therefore, we can write the above equation as
$\Rightarrow e=\dfrac{8}{10}$
We have to cancel the common factor 2 from the RHS of the above equation.
$\Rightarrow e=\dfrac{4}{5}$
We know that If an ellipse has centre $\left( 0,0 \right)$ ,eccentricity, e and semi-major axis, a in the x-direction, then the directrix is given by
$x=\pm \dfrac{a}{e}$
Let us substitute the value of a and e in the above equation.
$\begin{aligned} & \Rightarrow x=\pm \dfrac{10}{\dfrac{4}{5}} \\\ & \Rightarrow x=\pm 10\times \dfrac{5}{4} \\\ & \Rightarrow x=\pm \dfrac{50}{4} \\\ \end{aligned}$
Let us cancel the common factor of 2 from the RHS.
$\Rightarrow x=\pm \dfrac{25}{2}$
Let us take 2 from the RHS to the LHS to create an equation.
$\Rightarrow 2x=\pm 25$
Let us draw the graph of the given equation.

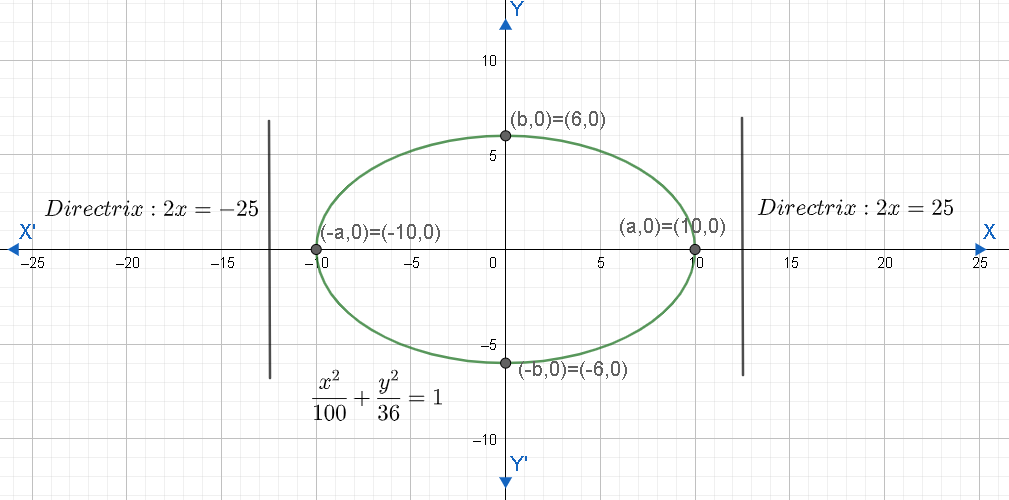
Hence, equation of the directrix of the ellipse $\dfrac{{{x}^{2}}}{100}+\dfrac{{{y}^{2}}}{36}=1$ is $2x=\pm 25$ .

Note: Students must be thorough with the formulas related to the ellipse. Here, we have used the standard form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ , when a is along x-axis. We know that for an ellipse $a>b$ . The largest value (a) comes along with x in the given equation $\dfrac{{{x}^{2}}}{100}+\dfrac{{{y}^{2}}}{36}=1$ . If the equation was of the form $\dfrac{{{x}^{2}}}{36}+\dfrac{{{y}^{2}}}{100}=1$ , we would have used the standard equation $\dfrac{{{x}^{2}}}{{{b}^{2}}}+\dfrac{{{y}^{2}}}{{{a}^{2}}}=1$ and the corresponding directrix can be found using the formula $y=\pm \dfrac{b}{e}$ .