Solveeit Logo
Login

Question

Question: Find the equation of the curve in Cartesian form \[x=-1+2\sin \theta ,y=1+2\cos \theta .\] Then find...

Find the equation of the curve in Cartesian form x=−1+2sin⁡θ,y=1+2cos⁡θ.x=-1+2\sin \theta ,y=1+2\cos \theta . Then find the centre and radius of the circle.

Explanation

Solution

To solve this question, we will calculate x + 1 and y – 1 then calculate the square of them using the formula (a+b)2=a2+2ab+b2{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}} and (a−b)2=a2−2ab+b2.{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}. Finally, we will add them to get an equation of the form ax2+by2+2hxy+2gx+2fy+c=0a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0 then the centre (−ga,−fa)\left( \dfrac{-g}{a},\dfrac{-f}{a} \right) and radius is 1ag2+f2−ac.\dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}.

Complete step-by-step answer:
We are given
x=−1+2sin⁡θ.....(i)x=-1+2\sin \theta .....\left( i \right)
y=1+2cos⁡θ.....(ii)y=1+2\cos \theta .....\left( ii \right)
Consider equation (i), first, we have,
x=−1+2sin⁡θx=-1+2\sin \theta
⇒x+1=2sin⁡θ\Rightarrow x+1=2\sin \theta
Squaring both the sides of the above equation, we get,
⇒(x+1)2=(2sin⁡θ)2\Rightarrow {{\left( x+1 \right)}^{2}}={{\left( 2\sin \theta \right)}^{2}}
⇒(x+1)2=4sin⁡2θ\Rightarrow {{\left( x+1 \right)}^{2}}=4{{\sin }^{2}}\theta
Using the identity of the square of two numbers given as
(a+b)2=a2+2ab+b2{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}
Using this in (x+1)2{{\left( x+1 \right)}^{2}} we have
(x+1)2=x2+2x+1{{\left( x+1 \right)}^{2}}={{x}^{2}}+2x+1
⇒(x+1)2=4sin⁡2θ\Rightarrow {{\left( x+1 \right)}^{2}}=4{{\sin }^{2}}\theta
⇒x2+2x+1=4sin⁡2θ.....(iii)\Rightarrow {{x}^{2}}+2x+1=4{{\sin }^{2}}\theta .....\left( iii \right)
Consider the equation (ii) now, we have,
y=1+2cos⁡θy=1+2\cos \theta
⇒y−1=2cos⁡θ\Rightarrow y-1=2\cos \theta
Squaring both the sides of the above equation, we have,
⇒(y−1)2=(2cos⁡θ)2\Rightarrow {{\left( y-1 \right)}^{2}}={{\left( 2\cos \theta \right)}^{2}}
⇒(y−1)2=4cos⁡2θ\Rightarrow {{\left( y-1 \right)}^{2}}=4{{\cos }^{2}}\theta
Now, we have an identity of the square of the difference of two numbers which is given by (a−b)2=a2−2ab+b2.{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}. Using this identity in (y−1)2,{{\left( y-1 \right)}^{2}}, we have,
(y−1)2=y2−2y+1{{\left( y-1 \right)}^{2}}={{y}^{2}}-2y+1
⇒(y−1)2=4cos⁡2θ\Rightarrow {{\left( y-1 \right)}^{2}}=4{{\cos }^{2}}\theta
⇒y2−2y+1=4cos⁡2θ.....(iv)\Rightarrow {{y}^{2}}-2y+1=4{{\cos }^{2}}\theta .....\left( iv \right)
To get the required equation of the curve, let us add the equation (iii) and equation (iv).
Equation (iii) is x2+2x+1=4sin⁡2θ.{{x}^{2}}+2x+1=4{{\sin }^{2}}\theta .
Equation (iv) is y2−2y+1=4cos⁡2θ.{{y}^{2}}-2y+1=4{{\cos }^{2}}\theta .
Adding these, we get,
x2+2x+1+y2−2y+1=4sin⁡2θ+4cos⁡2θ{{x}^{2}}+2x+1+{{y}^{2}}-2y+1=4{{\sin }^{2}}\theta +4{{\cos }^{2}}\theta
⇒x2+2x+y2−2y+2=4sin⁡2θ+4cos⁡2θ\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4{{\sin }^{2}}\theta +4{{\cos }^{2}}\theta
Using sin⁡2θ+cos⁡2θ=1,{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1, we get,
⇒x2+2x+y2−2y+2=4(sin⁡2θ+cos⁡2θ)\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4\left( {{\sin }^{2}}\theta +{{\cos }^{2}}\theta \right)
⇒x2+2x+y2−2y+2=4×1\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4\times 1
⇒x2+2x+y2−2y+2=4\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4
This is the required equation of the curve when x=−1+2sin⁡θx=-1+2\sin \theta and y=1+2cos⁡θ.y=1+2\cos \theta . This is a 2-degree equation, we have,
x2+y2+2x−2y+2−4=0{{x}^{2}}+{{y}^{2}}+2x-2y+2-4=0
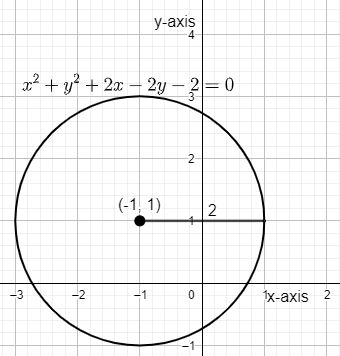
⇒x2+y2+2x−2y−2=0\Rightarrow {{x}^{2}}+{{y}^{2}}+2x-2y-2=0
Finally, we have to find the centre and radius of the circle from the obtained curve.
x2+y2+2x−2y−2=0.....(v){{x}^{2}}+{{y}^{2}}+2x-2y-2=0.....\left( v \right)
The general equation of the second degree is given by
ax2+2hxy+by2+2gx+2fy+c=0......(vi)a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0......\left( vi \right)
Here, the centre of the circle is given by (−ga,−fa)\left( \dfrac{-g}{a},\dfrac{-f}{a} \right) and the radius is given by 1ag2+f2−ac.\dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}.
So, finally, we will use this to get our result. Let us compare equations (v) and (vi).
⇒a=1;2=2g\Rightarrow a=1;2=2g
⇒b=1;2f=−2\Rightarrow b=1;2f=-2
⇒2h=0;c=−2\Rightarrow 2h=0;c=-2
⇒a=b=1,h=0,g=1,f=−1,c=−2\Rightarrow a=b=1,h=0,g=1,f=-1,c=-2
Then the centre of the circle is given by (−ga,−fa)=(−1,1).\left( \dfrac{-g}{a},\dfrac{-f}{a} \right)=\left( -1,1 \right). And the radius of our curve circle is given by
1ag2+f2−ac=11(1)2+(−1)2+2\dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}=\dfrac{1}{1}\sqrt{{{\left( 1 \right)}^{2}}+{{\left( -1 \right)}^{2}}+2}
⇒1ag2+f2−ac=4\Rightarrow \dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}=\sqrt{4}
⇒1ag2+f2−ac=2\Rightarrow \dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}=2
Hence, the curve is given by x2+y2+2x−2y−2=0{{x}^{2}}+{{y}^{2}}+2x-2y-2=0 and the centre is given by (– 1, 1) and radius = 2.

Note: Another method can be simply adding (x+1)2{{\left( x+1 \right)}^{2}} and (y−1)2{{\left( y-1 \right)}^{2}} and this gives (x+1)2+(y−1)2=4(sin⁡2θ+cos⁡2θ)=4×1=4.{{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4\left( {{\sin }^{2}}\theta +{{\cos }^{2}}\theta \right)=4\times 1=4. Then the required equation is (x+1)2+(y−1)2=(2)2.{{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{\left( 2 \right)}^{2}}. When the equation of the circle is of the form (x−a)2+(y−b)2=r2{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} then the centre is (a, b) and the radius = r. Comparing it from (x+1)2+(y−1)2=22{{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{2}^{2}} we have the centre as (– 1, 1) and the radius is 2 which is same as obtained above.