Question

Find the equation of the circles passing through the points of contact of direct common tangents of ${x^2} + {y^2} = 16$ and ${x^2} + {y^2} - 12x + 32 = 0$.

Answer 1

First of all, find the center and radius of the given circles. Then draw the figure for direct common tangents of the given circles by constructing the chords to get an idea of what we have to find. Further equate the equations of the two obtained circles as they are the same. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
Let the given circles are ${x^2} + {y^2} = 16$ and ${x^2} + {y^2} - 12x + 32 = 0$
We know that for the circle equation ${x^2} + {y^2} = {a^2}$ the center of the circle is $\left( {0,0} \right)$ and radius of the circle is $a$.
So, for the circle equation ${x^2} + {y^2} = 16$ he center is ${C_1}\left( {0,0} \right)$ and its radius is ${r_1} = 4$.
We also know that for the circle equation ${x^2} + {y^2} + 2gx + 2fy + c = 0$ the center of the circle is $\left( { - g, - f} \right)$ and radius of the circle is $\sqrt {{g^2} + {f^2} - c}$.
So, for the circle equation ${x^2} + {y^2} - 12x + 32 = 0$ the center is ${C_2}:\left( {6,0} \right)$ and its radius is ${r_2} = \sqrt {{{\left( { - 6} \right)}^2} + {0^2} - 32} = \sqrt {36 - 32} = \sqrt 4 = 2$.

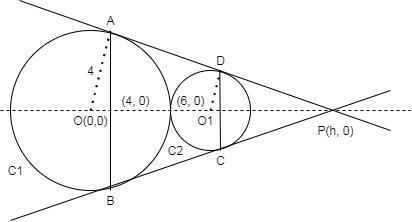
Clearly, the external center of similitude lies on the x-axis.
Since the external center of similitude lies on the x-axis let it be $P\left( {h,0} \right)$
The external center of similitude, $P\left( {h,0} \right)$ divides ${C_1}{C_2}$ in the ratio $4:2$ externally.
$\Rightarrow P\left( {h,0} \right) = \left( {\dfrac{{4\left( 6 \right) - 2\left( 0 \right)}}{{4 - 2}},\dfrac{{4\left( 0 \right) - 2\left( 0 \right)}}{{4 - 2}}} \right) = \left( {\dfrac{{24 - 0}}{2},\dfrac{0}{2}} \right) = \left( {12,0} \right)$
If A, B, C and D be the points of contact of direct common tangents, then AB and CD will be the chord of contacts of P with respect to circles ${C_1}$ and ${C_2}$, respectively.
Hence, the equation of AB is $x = \dfrac{4}{3}$ and the equation of CD is $x = \dfrac{{20}}{3}$.
Now, equation of any circle that can be drawn through the intersection of ${C_1}$ and AB is,

$$\Rightarrow {x^2} + {y^2} - 16 + {\lambda _1}\left( {x - \dfrac{4}{3}} \right) = 0 \\\ \Rightarrow {x^2} + {y^2} + {\lambda _1}x - \left( {16 + \dfrac{{4{\lambda _1}}}{3}} \right) = 0 \\\$$

And, equation of circle passing through the intersection of ${C_2}$ and CD is,

$$\Rightarrow {x^2} + {y^2} - 12x + 32 + {\lambda _2}\left( {x - \dfrac{{20}}{3}} \right) = 0 \\\ \Rightarrow {x^2} + {y^2} - 12x + {\lambda _2}x + \left( {32 - \dfrac{{20{\lambda _2}}}{3}} \right) = 0 \\\ \Rightarrow {x^2} + {y^2} + x\left( {{\lambda _2} - 12} \right) + \left( {32 - \dfrac{{20{\lambda _2}}}{3}} \right) = 0 \\\$$

Since these two circles should be same, we have
$\Rightarrow \dfrac{{{\lambda _2} - 12}}{{{\lambda _1}}} = \dfrac{{32 - \dfrac{{20{\lambda _2}}}{3}}}{{ - \left( {16 + \dfrac{{4{\lambda _1}}}{3}} \right)}} = 1$
By equating the first and last terms, we have

$$\Rightarrow \dfrac{{{\lambda _2} - 12}}{{{\lambda _1}}} = 1 \\\ \Rightarrow {\lambda _1} = {\lambda _2} - 12........................................\left( 1 \right) \\\$$

Equating the second and last terms, we have

$$\Rightarrow 32 - \dfrac{{20{\lambda _2}}}{3} = - 16 - \dfrac{{4{\lambda _1}}}{3} \\\ \Rightarrow 96 - 20{\lambda _2} = - 48 - 4{\lambda _1} \\\ \Rightarrow 96 - 20{\lambda _2} = - 48 - 4\left( {{\lambda _2} - 12} \right){\text{ }}\left[ {\because {\text{using }}\left( 1 \right)} \right] \\\ \Rightarrow 96 - 20{\lambda _2} = - 48 - 4{\lambda _2} + 48 \\\ \Rightarrow 96 = 20{\lambda _2} - 4{\lambda _2} \\\ \Rightarrow 96 = 16{\lambda _2} \\\ \therefore {\lambda _2} = 6 \\\$$

Substituting ${\lambda _2} = 6$ in equation (1), we get

$$\Rightarrow {\lambda _1} = 6 - 12 \\\ \therefore {\lambda _1} = - 6 \\\$$

Substituting ${\lambda _1} = - 6$ in ${x^2} + {y^2} - 6x - \left( {16 + \dfrac{{4\left( { - 6} \right)}}{3}} \right) = 0$ we get

$$\Rightarrow {x^2} + {y^2} - 6x - \left( {16 + \dfrac{{4\left( { - 6} \right)}}{3}} \right) = 0 \\\ \Rightarrow {x^2} + {y^2} - 6x - 16 + 8 = 0 \\\ \therefore {x^2} + {y^2} - 6x - 8 = 0 \\\$$

Note: A circle is a round plane figure whose boundary consists of points equidistant from a fixed point, i.e., the center. A tangent is a straight line or plan that touches a curve or curved surface at a point, but if extended does not cross it at that point. While solving these types of questions one should be focused and must remember all the formulas.