Question

Find the equation of the circle which touches the circle ${{x}^{2}}+{{y}^{2}}-6x+6y+17=0$ externally and to which the lines ${{x}^{2}}-3xy-3x+9y=0$ are normal.
A. ${{x}^{2}}+{{y}^{2}}+6x-2y+1=0$
B. ${{x}^{2}}+{{y}^{2}}-6x+2y+1=0$
C. ${{x}^{2}}+{{y}^{2}}-6x-2y+1=0$
D. None of these.

Answer 1

For solving this type of question you should know about the concept of circle and the normal and lines. In this we derive the intersection points by the equation of the line and then by the equation of the circle, we find the centre and by the help of these points we calculate the radius of the circle and then will find the equation of the circle.

Complete step by step answer:
So, the required circle is touching externally to the circle ${{x}^{2}}+{{y}^{2}}-6x+6y+17=0$ and has a normal line ${{x}^{2}}-3xy-3x+9y=0$.By the equation of the normal line,
$\begin{aligned} & \Rightarrow {{x}^{2}}-3xy-3x+9y=0 \\\ & \Rightarrow \left( x-3 \right)\left( x-3xy \right)=0 \\\ \end{aligned}$
So, this is equation for the lines $x-3=0$ and $x-3xy=0$. So, the intersection of these lines is at the point $P\left( 3,1 \right)$. We found it by calculating the equation of both lines. So, both lines are the normal to the circle. And this implies that the intersection of both of these lines is the centre of the required circle.
So, the centre for the required circle is $P\left( 3,1 \right)$ and the circle which is touching our required circle is ${{x}^{2}}+{{y}^{2}}-6x+6y+17=0$.
For the centre of this circle,
$\Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=1$

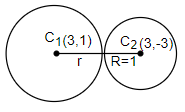
So, the circle’s centre is $Q\left( 3,-3 \right)$ and the radius for this circle is 1. The distance between these two circles is the distance between the two points, $P\left( 3,1 \right)$ and $Q\left( 3,-3 \right)$. So, the distance between these is 4.
$\Rightarrow$ for the radius of required circle = 4 - 1 = 3.
So, the equation for the required circle with centre $P\left( 3,1 \right)$ and radius 3 is,
$\begin{aligned} & {{\left( x-3 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{3}^{2}} \\\ & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=9 \\\ \end{aligned}$
By solving this equation, we get,
${{x}^{2}}+{{y}^{2}}-6x-2y+1=0$
So, the correct answer is “Option C”.

Note: During solving this question you should be careful about determining the values of the centre. And if one normal line is given then apply it for both and if two circles are touching each other then they will definitely give some common values which will be used for solving the next circle or required circle.