Question

Find the equation of the circle which passes through the point (1, 2), (2, 2) and (4, – 1).

Answer 1

Hint: First we will find the center and radius of the circle using distance formula and then we will find the equation of the circle from obtained data
Distance Formula, $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

Complete step-by-step answer:
Given that points (1, 2), (2, 2) and (4, – 1) are lying on the given circle.
Let us assume point A (1, 2), point B (2, 2) and point C (4, – 1).
Also, assume that the center of the circle is O.
Coordinates of the center of the circle are (h, k).

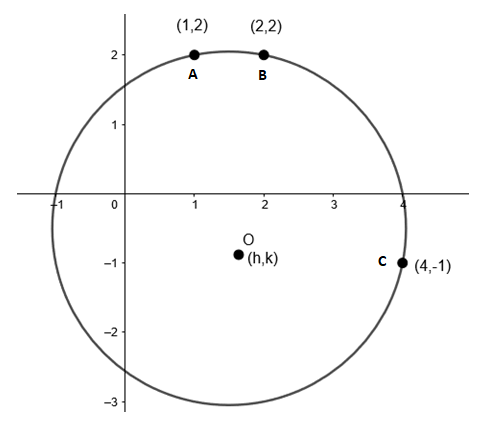
Now, we know that the radius of the circle is of equal length.
Thus, applying this property of the circle,
We get, AO = BO = CO
These are the radii of the circle, thus all are of equal length.
Also, from distance formula, the distance between two points, i.e. $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$
$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
where, d is the distance between two points.
Applying this between AO and BO as both are the radii of the circle,
$AO=BO$
$\Rightarrow \sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-2 \right)}^{2}}}=\sqrt{{{\left( h-2 \right)}^{2}}+{{\left( k-2 \right)}^{2}}}$
$\Rightarrow \sqrt{{{h}^{2}}+{{1}^{2}}-2\left( 1 \right)\left( h \right)+{{k}^{2}}+{{1}^{2}}-2\left( 1 \right)\left( k \right)}=\sqrt{{{h}^{2}}+{{2}^{2}}-2\left( 2 \right)\left( h \right)+{{k}^{2}}+{{2}^{2}}-2\left( 2 \right)\left( k \right)}$
$\Rightarrow \sqrt{{{h}^{2}}+1-2h+{{k}^{2}}+4-4k}=\sqrt{{{h}^{2}}+4-4h+{{k}^{2}}+4-4k}$
$\Rightarrow \sqrt{{{h}^{2}}+{{k}^{2}}-2h-4k+5}=\sqrt{{{h}^{2}}+{{k}^{2}}-4h-4k+8}$
Squaring both sides, we get
$\Rightarrow {{h}^{2}}+{{k}^{2}}-2h-4k+5={{h}^{2}}+{{k}^{2}}-4h-4k+8$
Canceling the similar terms, from both sides, we get,
$\Rightarrow -2h-4k+5=-4h-4k+8$
$\Rightarrow -2h+4h-4k+4k=8-5$
$\Rightarrow 2h=3$
$\Rightarrow h=\dfrac{3}{2}$
$\Rightarrow h=1.5$
Similarly,
$AO=CO$
$\Rightarrow \sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-2 \right)}^{2}}}=\sqrt{{{\left( h-4 \right)}^{2}}+{{\left( k-\left( -1 \right) \right)}^{2}}}$
$\Rightarrow \sqrt{{{h}^{2}}+{{1}^{2}}-2\left( 1 \right)\left( h \right)+{{k}^{2}}+{{2}^{2}}-2\left( 2 \right)\left( k \right)}=\sqrt{{{h}^{2}}+{{4}^{2}}-2\left( 4 \right)\left( h \right)+{{k}^{2}}+{{1}^{2}}-2\left( k \right)\left( -1 \right)}$
$\Rightarrow \sqrt{{{h}^{2}}+1-2h+{{k}^{2}}+4-4k}=\sqrt{{{h}^{2}}+16-8h+{{k}^{2}}+1+2k}$
Squaring both sides, we get
$\Rightarrow {{h}^{2}}+1-2h+{{k}^{2}}+4-4k={{h}^{2}}+16-8h+{{k}^{2}}+1+2k$
$\Rightarrow {{h}^{2}}+{{k}^{2}}-2h-4k+5={{h}^{2}}+{{k}^{2}}-8h+2k+17$
Canceling similar terms from both sides, we get
$\Rightarrow -2h-4k+5=-8h+2k+17$
$\Rightarrow -2h+8h-4k-2k=17-5$
$\Rightarrow 6h-6k=12$
$h-k=2.....\left( i \right)$
Also, we know that the value of h as 1.5.
So, putting the value of h = 1.5 in equation (i), we get
$\Rightarrow 1.5-k=2$
$\Rightarrow -k=0.5$
$\Rightarrow k=-0.5$
Now, we have the coordinates of the center of the circle, i.e. O (h, k).
$h=1.5,\text{ }k=-0.5$
$\left( h,k \right)=\left( 1.5,-0.5 \right)$
We know that OA is the radius of the circle.
So, by putting the value of (h, k) in the distance formula of OA, we can find the radius of the given circle.
$OA=\sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-2 \right)}^{2}}}$
$OA=\sqrt{{{\left( 1.5-1 \right)}^{2}}+{{\left( -0.5-2 \right)}^{2}}}$
$OA=\sqrt{{{\left( 1.5 \right)}^{2}}+{{\left( 1 \right)}^{2}}-2\left( 1.5 \right)\left( 1 \right)+{{\left( -0.5 \right)}^{2}}+{{\left( 2 \right)}^{2}}-2\left( -0.5 \right)\left( 2 \right)}$
$OA=\sqrt{2.25+1-3+0.25+4+2}$
$OA=\sqrt{6.50}$
Squaring both sides, we get
$O{{A}^{2}}=6.50$
${{\left( r \right)}^{2}}=6.50$
${{\left( OA \right)}^{2}}={{\left( r \right)}^{2}}$
The radius of the circle.
Now, we are ready with all the required values to form an equation of the circle.
We know that the general equation of the circle is ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}$
Putting the values of (h, k) and ${{\left( r \right)}^{2}}$, we get
$\Rightarrow {{\left( x-1.5 \right)}^{2}}+{{\left( y-\left( -0.5 \right) \right)}^{2}}=6.50$
$\Rightarrow {{x}^{2}}+{{\left( 1.5 \right)}^{2}}-2\left( x \right)\left( 1.5 \right)+{{y}^{2}}+{{\left( 0.5 \right)}^{2}}+2\left( y \right)\left( 0.5 \right)=6.50$
$\Rightarrow {{x}^{2}}+2.25-3x+{{y}^{2}}+0.25+y=6.50$
$\Rightarrow {{x}^{2}}+{{y}^{2}}-3x+y+2.50-6.50=0$
$\Rightarrow {{x}^{2}}+{{y}^{2}}-3x+y-4=0$

Note: Alternate Method:
We can solve this question by using the following steps.
1. Substitute the values of the given point in the general equation of the circle.
2. Find the values of the unknowns i.e. (h, k) and r.
3. Form the required equation of the circle.