Question

Find the equation of the circle which cuts the following circles orthogonally.

& {{x}^{2}}+{{y}^{2}}+4x-7=0 \\\ & 2{{x}^{2}}+2{{y}^{2}}+3x+5y-9=0 \\\ & {{x}^{2}}+{{y}^{2}}+y=0 \\\ \end{aligned}$$

Answer 1

For solving this question we will use the concept of orthogonal circles or orthogonal curves. In this question we will use formula $2{{g}_{i}}g+2{{f}_{i}}f={{c}_{i}}+c$ where ${{g}_{i}},{{f}_{i}},{{c}_{i}}\left( i=1,2,3 \right)$ are the terms occurring in standard equation given circles ${{x}^{2}}+{{y}^{2}}+2{{g}_{i}}x+2{{f}_{i}}y+{{c}_{i}}=0\,\,\,\,$ and then substitute the values of different g, f and c in the formula and solve the equations accordingly.$$$$

Complete step-by-step answer:

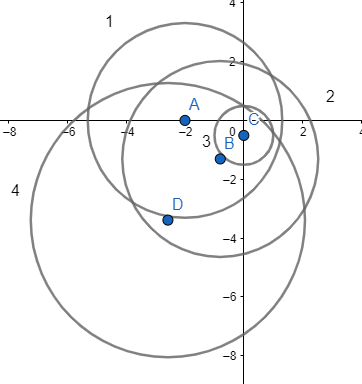
In the above figure point, A is the center of the circle (1), point B is the center of the circle (2), point C is the center of the circle (3), point D is the center of the circle (4) which cut all the other three circles orthogonally.
Two circles are said to be orthogonal circles if the tangent at their point of intersection is at right angles.$$$$
If two circles are cut orthogonally then it must satisfy the following condition:
$2{{g}_{i}}g+2{{f}_{i}}f={{c}_{i}}+c$
Equation of given circles:

& {{x}^{2}}+{{y}^{2}}+4x-7=0\,\,\,\,\,\,\,\,\,.....(1) \\\ & 2{{x}^{2}}+2{{y}^{2}}+3x+5y-9=0\,\, \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+\dfrac{3}{2}x+\dfrac{5}{2}y-\dfrac{9}{2}=0\,\,\,\,\,\,\,\,.....(2) \\\ & {{x}^{2}}+{{y}^{2}}+y=0\,\,\,\,\,\,\,.....(3) \\\ \end{aligned}$$ Let us assume a circle which cuts the following circles orthogonally be: $$ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\,\,\,\,\,\,.....(4)$$ Where $-g$ and $-f$ are the coordinates of the centre of a circle. Point A is the centre of circle (1), point B is the centre of circle (2), point C is the centre of circle (3), point D is the centre of circle (4) and all the three circles cut all the other three circles orthogonally. On comparing circle (1), circle (2) and circle (3) with circle (4), we get, $$ \begin{aligned} & {{g}_{1}}=-2,\,{{f}_{1}}=0\,,\,{{c}_{1}}=-7\, \\\ & {{g}_{2}}=\dfrac{-3}{4},\,{{f}_{2}}=\dfrac{-5}{4},\,{{c}_{2}}=\dfrac{-9}{2}\, \\\ & {{g}_{3}}=0,\,{{f}_{3}}=\dfrac{-1}{2}\,,\,{{c}_{3}}=0 \\\ \end{aligned}$$ We know that two circles intersect orthogonally if: $$ 2{{g}_{i}}g+2{{f}_{i}}f={{c}_{i}}+c\,\,\,\,\,\,\,\,\ldots ..\text{ }\left( 5 \right)$$ Taking circle (1) and circle (4), we have${{g}_{1}}=-2,\,{{f}_{1}}=0\,,\,{{c}_{1}}=-7\,;\,g=g,\,f=f,\,c=c$.Substituting values of g, f and c in equation (5) we get, $$ \begin{aligned} & 2(-2)(g)+2(0)(f)=-7+c \\\ & \Rightarrow 4g=-7+c \\\ & \Rightarrow c+4g=7......\left( 6 \right) \\\ \end{aligned}$$ Now we take circle (2) and circle (4) and we have${{g}_{2}}=\dfrac{-3}{4},\,{{f}_{2}}=\dfrac{-5}{4}\,,\,{{c}_{2}}=-\dfrac{9}{2}\,;\,g=g,\,f=f,\,c=c$, substituting values of g, f and c in equation (5) we get, $$ \begin{aligned} & 2\left( \dfrac{-3}{4} \right)(g)+2\left( \dfrac{-5}{4} \right)(f)=-\dfrac{9}{2}+c \\\ & \Rightarrow \dfrac{-3}{2}g-\dfrac{5}{2}f=\dfrac{2c-9}{2} \\\ & \Rightarrow -3g-5f=2c-9 \\\ & \Rightarrow 2c+3g+5f=9\,\,\,\,\,\,\,\,\ldots ..\text{ }\left( 7 \right) \\\ \end{aligned} $$ Now we take circle (3) and circle (4).We have${{g}_{3}}=0,\,{{f}_{3}}=\dfrac{-1}{2}\,,\,{{c}_{3}}=0\,;\,g=g,\,f=f,\,c=c$. Substituting values of g, f and c in equation (5) we get, $$ \begin{aligned} & 2(0)(g)+2\left( \dfrac{-1}{2} \right)(f)=0+c \\\ & \Rightarrow -f=c\,\,\,\,\,\,\ldots ..\text{ }\left( 8 \right) \\\ \end{aligned}$$ Putting equation (8) in equation (6) we get, $$ 4g-f=7\,\,\,\,\,\,\,\ldots ..\text{ }\left( 9 \right)$$ Putting equation (8) in equation (7) we get, $$ \begin{aligned} & -2f+3g+5f=9 \\\ & \Rightarrow 3g+3f=9 \\\ & \Rightarrow g+f=3 \\\ & \Rightarrow f=3-g\,\,\,\,\,\,\ldots ..\text{ }\left( 10 \right) \\\ \end{aligned}$$ Putting equation (10) in equation (9) we get, $$ \begin{aligned} & 4g-(3-g)=7 \\\ & \Rightarrow 5g=10 \\\ & \Rightarrow g=2\,\,.....(11) \\\ \end{aligned}$$ Putting equation (11) in equation (10) we get, $$ \Rightarrow f=3-2=1.....(12) $$ Putting equation (12) in equation (8) we get, $$ \begin{aligned} & -1=c \\\ & \Rightarrow c=-1.....(13)\\\ \end{aligned}$$ Substituting equation (11), equation (12) and equation (13) in circle (4) we get: $$ \begin{aligned} & {{x}^{2}}+{{y}^{2}}+2\times 2x+2\times 1\times y-1=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+4x+2y-1=0 \\\ \end{aligned} $$ Hence, circle required to cut the following circles orthogonally is ${{x}^{2}}+{{y}^{2}}+4x+2y-1=0$. $$$$ **Note:** We note the centre of the circle is at $\left( -g,-f \right)=\left( -2,-1 \right)$ and radius $\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{6}$ .We can alternatively obtained the equation of the circle in centre-radius from by finding radical axis and then the radical centre lying on it and then the radius as the perpendicular distance from centre to its tangent. We also note that we have to convert the coefficient of ${{x}^{2}},{{y}^{2}}$ to 1 to find the centre of the circles.