Question

Find the equation of the circle passing through the three non-collinear points $\left( 1,1 \right),\left( 2,-1 \right)$ and $\left( 3,2 \right)$.

Answer 1

Hint: We will put the given points in the general equation of the circle and find the values of $\left( g,f \right)$ and $c$ and then form the required equation of the circle.

Given that $\left( 1,1 \right),\left( 2,-1 \right)$ and $\left( 3,2 \right)$ are three non-collinear points. All of these non-collinear points lie on the circle.
We have to find the equation of the given circle.

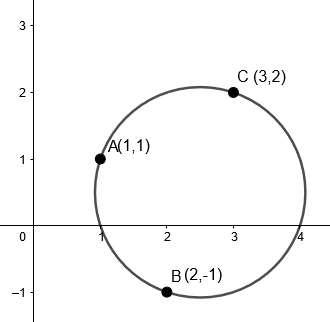
We know that the general equation of the circle is
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
All of these non-collinear points lie on the circle.
Putting the values of point $A\left( 1,1 \right)$ in the general equation of the circle, we get
$\Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
$\Rightarrow {{1}^{2}}+{{1}^{2}}+2g\left( 1 \right)+2f\left( 1 \right)+c=0$
$\Rightarrow 1+1+2g+2f+c=0$
$\Rightarrow 2+2g+2f+c=0$
$\Rightarrow 2g+2f+c=-2.....\left( i \right)$
Putting the value of point $B\left( 2,-1 \right)$ in the general equation of the circle, we get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
$\Rightarrow {{2}^{2}}+{{\left( -1 \right)}^{2}}+2g\left( 2 \right)+2f\left( -1 \right)+c=0$
$\Rightarrow 4+1+4g-2f+c=0$
$\Rightarrow 4g-2f=-c-5.....\left( ii \right)$
Putting the value of point $C\left( 3,2 \right)$ in the general equation of the circle, we get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
$\Rightarrow {{3}^{2}}+{{\left( 2 \right)}^{2}}+2g\left( 3 \right)+2f\left( 2 \right)+c=0$
$\Rightarrow 9+4+6g+4f+c=0$
$\Rightarrow 6g+4f=-c-13.....\left( iii \right)$
Now, we have three equations and three unknowns i.e. $g,f$ and $c$ respectively.
Solving equation $\left( i \right)$ and $\left( ii \right)$, we get

& 2g+2f=-c-2 \\\ & \underline{4g-2f=-c-5} \\\ & 6g+0=-2c-7 \\\ \end{aligned}$$ Putting the value of $$6g$$ in equation $$\left( iii \right)$$, $$\Rightarrow 6g+4f=-c-13$$ $$\Rightarrow -2c-7+4f=-c-13$$ $$\Rightarrow 4f=c-6$$ $$\Rightarrow c=4f+6$$ Now, putting the value of $$c$$ in the equation $$\left( i \right)$$, we get $$\Rightarrow 2g+2f=-4f-6-2$$ $$\Rightarrow 2g+2f=-4f-8$$ $$\Rightarrow 2g+6f=-8.....\left( v \right)$$ Putting the value of $$'c'$$ from the equation $$\left( iv \right)$$ in the equation $$\left( ii \right)$$, we get $$\Rightarrow 4g-2f=-4f-6-5$$ $$\Rightarrow 4g+2f=-11.....\left( vi \right)$$ Solving equation $$\left( v \right)$$ and $$\left( vi \right)$$, we get $$\begin{aligned} & 4g+12f=-16 \\\ & 4g+2f=-11 \\\ & \underline{-\text{ - + }} \\\ & 0+10f=-5 \\\ \end{aligned}$$ $$f=-\dfrac{1}{2}$$ Put the value of $$f$$in the equation $$\left( v \right)$$, we get $$2g+6\times \left( -\dfrac{1}{2} \right)=-8$$ $$g=\dfrac{-8+3}{2}$$ $$g=\dfrac{-5}{2}$$ Similarly, putting the value of $$f$$ in the equation $$\left( iv \right)$$, we get $$\Rightarrow c=4f+6$$ $$\Rightarrow c=4\times \left( \dfrac{-1}{2} \right)+6$$ $$\Rightarrow c=4$$ Now, we have all the required points to form an equation of the circle. Thus, by putting the values in the general equation of the circle, we get $$\Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$$ $$\Rightarrow {{x}^{2}}+{{y}^{2}}+2\left( \dfrac{-5}{2} \right)x+2\left( \dfrac{-1}{2} \right)y+4=0$$ $$\Rightarrow {{x}^{2}}+{{y}^{2}}-5x-y+4=0$$ Note: Alternative method: You can solve this question by using the distance formula $$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$$ $$d$$ is the distance between two points. By putting the values of the given point in the distance formula, we can find the coordinates of the circle and its radius and finally the required equation of the circle.