Question

Find the equation of the circle passing through $\left( 0,0 \right)$ and making intercepts $a$ and $b$ on the coordinate axes.

Answer 1

We denote the centre of the circle as $C\left( h,k \right)$ and radius $OA=r$ where O is the origin. We use given intercepts $a,b$ and find the coordinates of $A,B$ where $x-$ and $y-$ axis cut the circle excluding O. We put the coordinates of $A,B,O$ in the equation of the circle in centre-radius to express $h,k,{{r}^{2}}$ in terms of $a,b$ . We put the expressions in $a,b$ centre-radius equation of circle to get the required.

Complete step-by-step answer:
Let us denote the centre of the given circle in the question as $C\left( h,k \right)$ and the radius as $OA=r$ where O is the origin. Let $x-$ axis cut circle excluding the origin at A and $y-$ axis cut circle excluding the origin at B . So we have obtained the $x-$ intercept OA and $y-$ intercept OB. We are given i the question that $a$ and $b$ are length of the intercept. We assign
$OA=a,OB=b$
So the co-ordinates of A and B are given by $A\left( a,0 \right),B\left( 0,b \right)$ . $$$$

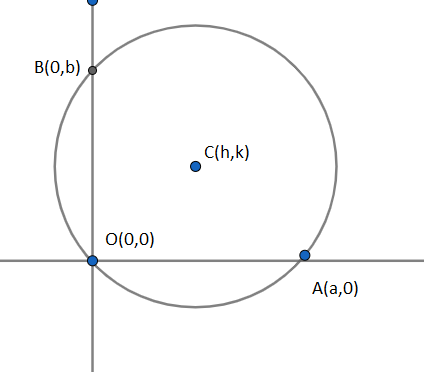
We write the equation of the circle in centre radius form as
${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}......\left( 1 \right)$
The circle (1) passes through origin $O\left( 0,0 \right)$ and so $O\left( 0,0 \right)$ will satisfy equation of circle (1). So we have,

& {{\left( 0-h \right)}^{2}}+{{\left( 0-k \right)}^{2}}={{r}^{2}}. \\\ & \Rightarrow {{h}^{2}}+{{k}^{2}}={{r}^{2}}......\left( 2 \right) \\\ \end{aligned}$$ The circle (1) passes through origin $ A\left( a,0 \right) $ and so $ A\left( a,0 \right) $ will satisfy equation of circle (1). So we have, $$\begin{aligned} & {{\left( a-h \right)}^{2}}+{{\left( 0-k \right)}^{2}}={{r}^{2}}. \\\ & \Rightarrow {{a}^{2}}-2ah+{{h}^{2}}+{{k}^{2}}={{r}^{2}} \\\ & \Rightarrow {{a}^{2}}-2ah+{{r}^{2}}={{r}^{2}}\left( \because {{h}^{2}}+{{k}^{2}}={{r}^{2}} \right) \\\ & \Rightarrow a\left( a-2h \right)=0 \\\ \end{aligned}$$ So we have $ a=0 $ or $ h=\dfrac{a}{2} $ . If $ a=0 $ the point is on $ x- $ axis and we reject the value. So the $ x- $ coordinate of the centre is $ h=\dfrac{a}{2} $ . The circle (1) passes through origin $ B\left( 0,b \right) $ and so $ A\left( 0,b \right) $ will satisfy equation of circle (1). So we have, $$\begin{aligned} & {{\left( 0-h \right)}^{2}}+{{\left( b-k \right)}^{2}}={{r}^{2}}. \\\ & \Rightarrow {{h}^{2}}+{{b}^{2}}-2kb+{{k}^{2}}={{r}^{2}} \\\ & \Rightarrow {{b}^{2}}-2kb+{{r}^{2}}={{r}^{2}}\left( \because {{h}^{2}}+{{k}^{2}}={{r}^{2}} \right) \\\ & \Rightarrow b\left( b-2k \right)=0 \\\ \end{aligned}$$ So we have $ b=0 $ or $ k=\dfrac{b}{2} $ . If $ b=0 $ the point is on $ y- $ axis and we reject the value. So the $ y- $ coordinate of the centre is $ k=\dfrac{b}{2} $ . Let us put the value of $ h=\dfrac{a}{2},k=\dfrac{b}{2} $ in the equation (2) and find $ {{r}^{2}} $ . We have $$\begin{aligned} & {{\left( \dfrac{a}{2} \right)}^{2}}+{{\left( \dfrac{b}{2} \right)}^{2}}={{r}^{2}} \\\ & \Rightarrow {{r}^{2}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\\ \end{aligned}$$ We put the obtained values of $ h,k,{{r}^{2}} $ in equation(1) and have $$\begin{aligned} & {{\left( x-\dfrac{a}{2} \right)}^{2}}+{{\left( y-\dfrac{b}{2} \right)}^{2}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\\ & \Rightarrow {{x}^{2}}-ax+\dfrac{{{a}^{2}}}{4}+{{y}^{2}}-bx+\dfrac{{{b}^{2}}}{4}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\\ & \Rightarrow {{x}^{2}}-ax+{{y}^{2}}-bx+\dfrac{{{a}^{2}}+{{b}^{2}}}{4}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\\ & \Rightarrow {{x}^{2}}-ax+{{y}^{2}}-bx=0 \\\ \end{aligned}$$ The above equation is the required equation of the circle. $$$$ **Note:** We can also proceed to find the equation of the circle with $ x- $ intercept as $ b $ and h $ y- $ intercept as $ a $ and get the equation as $ {{x}^{2}}-bx+{{y}^{2}}-ay=0 $ . The general equation of circle in two variables is given by $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ for real numbers $ f,g,c $ which simultaneously cannot be zero and $ {{g}^{2}}+{{f}^{2}} > c $ .