Question

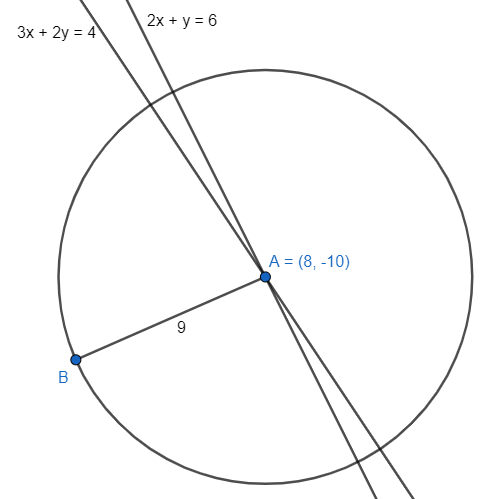
Find the equation of the circle if the equations of two diameters are $2x+y=6$ and $3x+2y=4$ when the radius of the circle is 9 cm.

Answer 1

We first find the general form of the circle as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. The intersecting point of any given diameters will give the centre. We use the radius and the centre in the equation to find the equation of the circle.

Complete step by step answer:
To find an equation of a circle we need at least the centre of the circle and its radius.
The general equation in that case is ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where $\left( a,b \right)$ is the centre and $r$ is the length of the radius.
It is given that the radius of the circle is 9 cm. Also, we are given the equation of two diameters which are $2x+y=6....(i)$ and $3x+2y=4.....(ii)$.
We know that the intersecting point of any two diameters will be the centre.
We multiply 2 to the both sides of the first equation and get
$\begin{aligned} & 2\times \left( 2x+y \right)=6\times 2 \\\ & \Rightarrow 4x+2y=12 \\\ \end{aligned}$
We take the equation as $4x+2y=12.....(iii)$.
Now we subtract the equation (ii) from equation (iii) and get $\left( 4x+2y \right)-\left( 3x+2y \right)=12-4$.
We take the variables together and the constants on the other side.
Simplifying the equation, we get
$\begin{aligned} & \left( 4x+2y \right)-\left( 3x+2y \right)=12-4 \\\ & \Rightarrow x=8 \\\ \end{aligned}$
The value of $x$ is 8. Now putting the value in the equation $2x+y=6....(i)$, we get
$\begin{aligned} & 2x+y=6 \\\ & \Rightarrow y=6-2\times 8=-10 \\\ \end{aligned}$.
Therefore, the centre is $\left( 8,-10 \right)$.
The equation of the circle is ${{\left( x-8 \right)}^{2}}+{{\left( y+10 \right)}^{2}}={{9}^{2}}$. Its simplified form will be
$\begin{aligned} & {{\left( x-8 \right)}^{2}}+{{\left( y+10 \right)}^{2}}={{9}^{2}} \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-16x+20y+83=0 \\\ \end{aligned}$
The equation of the circle is ${{x}^{2}}+{{y}^{2}}-16x+20y+83=0$.

Note: The general equation of any conic is $a{{x}^{2}}+bxy+c{{y}^{2}}+dx+ey+f=0$. In the case of a circle, the constants become specific where we get $a=c;b=0$. This gives us the equation of the circle. In general, it is defined as the curve formed from a plane’s intersection with a right circular cone.