Question

Find the equation of the circle circumscribing the triangle formed by the lines x + y = 6, 2x + y = 4 and x + 2y = 5.

Answer 1

Hint: We will find the vertices of the triangle formed by the given lines and then we will find the center and radius of the circle using the distance formula. Finally, we will find the required equation of the circle from the obtained data.
Distance formula, $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

Complete step-by-step answer:
Given that x + y = 6, 2x + y = 4 and x + 2y = 5 are the equation of the sides of a triangle. We have to find the equation of a circle circumscribing the triangle formed by the lines respectively.

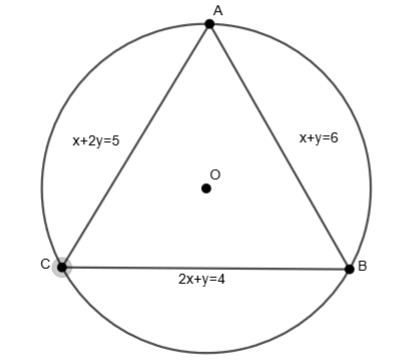
Let us assume that
$\Rightarrow x+y=6.....\left( i \right)$
$\Rightarrow 2x+y=4.....\left( ii \right)$
$\Rightarrow x+2y=5....\left( iii \right)$
Now, we will try to find out the vertices of $\Delta ABC$ as the vertices of the $\Delta ABC$ lie on the circle.
For finding the point A, we will solve the equation (i) and (iii) respectively, we get

& x+y=6 \\\ & x+2y=5 \\\ & \underline{-\text{ }} \\\ & 0+\left( -y \right)=1 \\\ \end{aligned}$$ $$y=-1$$ By putting the value of y in the equation (i), we get $$x+\left( -1 \right)=6$$ $$x=7$$ Thus, the point A is (7, – 1). Similarly, for point B, we will solve the equation (i) and (ii) respectively, we get $$\begin{aligned} & x+y=6 \\\ & 2x+y=4 \\\ & \underline{-\text{ }} \\\ & -x+0=2 \\\ \end{aligned}$$ $$x=-2$$ On putting the value of x = – 2 in the equation (i), we get $$-2+y=6$$ $$y=6+2$$ $$y=8$$ Thus, the point B is (– 2, 8). Similarly, for point C, we will solve the equation (iii) and (ii) respectively, we get $$\begin{aligned} & 2x+y=4 \\\ & \underline{x+2y=5} \\\ \end{aligned}$$ Multiplying equation (ii) with 2 on both sides, we get $$\begin{aligned} & 4x+2y=8 \\\ & \underline{\begin{aligned} & x+2y=5 \\\ & \- \\\ \end{aligned}} \\\ & 3x+0=3 \\\ \end{aligned}$$ $$x=\dfrac{3}{3}$$ $$x=1$$ Putting the value of x = 1 in the equation (iii), we get $$x+2y=5$$ $$1+2y=5$$ $$2y=4$$ $$y=2$$ Thus, the point C is (– 1, 2). Now, we have three points A (7, – 1), B (– 2, 8) and C (1, 2) which are lying on the circle. It means that the point must be satisfying the general equation of the circle. Now, we know that the general equation of the circle is: $${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}$$ Here, (h, k) are the coordinates of the circle and r is the radius of the circle. We know that radii of a circle are of equal length. Thus, from this we have $$O{{A}^{2}}=O{{B}^{2}}=O{{C}^{2}}$$ These are the radii of the same circle. Also, we know that the distance formula of two points $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)$$ is $$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$$ Applying distance formula between OA and OC, we get $$OA=OC$$ $$\Rightarrow \sqrt{{{\left( h-7 \right)}^{2}}+{{\left( k-\left( -1 \right) \right)}^{2}}}=\sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-2 \right)}^{2}}}$$ $$\Rightarrow \sqrt{{{h}^{2}}+{{\left( 7 \right)}^{2}}-2\left( 7 \right)\left( h \right)+{{k}^{2}}+{{1}^{2}}+2\left( k \right)\left( 1 \right)}=\sqrt{{{h}^{2}}+{{1}^{2}}-2\left( h \right)\left( 1 \right)+{{k}^{2}}+{{2}^{2}}-2\left( 2 \right)\left( k \right)}$$ $$\Rightarrow \sqrt{{{h}^{2}}+49-14h+{{k}^{2}}+1+2k}=\sqrt{{{h}^{2}}+1-2h+{{k}^{2}}+4-4k}$$ On squaring both sides, we get $$\Rightarrow {{h}^{2}}+{{k}^{2}}-14h+2k+50={{h}^{2}}+{{k}^{2}}-2h-4k+5$$ Canceling the like terms from both the sides, we get $$\Rightarrow -14h+2k+50=-2h-4k+5$$ $$\Rightarrow -14h+2h+2k+4k=5-50$$ $$\Rightarrow -12h+6k=-45$$ $$\Rightarrow 12h-6k=45....\left( iv \right)$$ Similarly, for OB = OC, $$\Rightarrow \sqrt{{{\left( h-\left( -2 \right) \right)}^{2}}+{{\left( k-8 \right)}^{2}}}=\sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-2 \right)}^{2}}}$$ $$\Rightarrow \sqrt{{{h}^{2}}+{{\left( 2 \right)}^{2}}-2\left( -2 \right)\left( h \right)+{{k}^{2}}+{{8}^{2}}-2\left( k \right)\left( 8 \right)}=\sqrt{{{h}^{2}}+{{1}^{2}}-2\left( h \right)\left( 1 \right)+{{k}^{2}}+{{2}^{2}}-2\left( 2 \right)\left( k \right)}$$ $$\Rightarrow \sqrt{{{h}^{2}}+4+4h+{{k}^{2}}+64-16k}=\sqrt{{{h}^{2}}+1-2h+{{k}^{2}}+4-4k}$$ $$\Rightarrow \sqrt{{{h}^{2}}+{{k}^{2}}+4h-16k+68}=\sqrt{{{h}^{2}}+{{k}^{2}}-2h-4k+5}$$ On squaring both sides, we get $${{h}^{2}}+{{k}^{2}}+4h-16k+68={{h}^{2}}+{{k}^{2}}-2h-4k+5$$ Canceling the similar terms from both the sides, we get $$\Rightarrow 4h-16k+68=-2h-4k+5$$ $$\Rightarrow 4h+2h-16k+4k=5-68$$ $$\Rightarrow 6h-12k=-63.....\left( v \right)$$ And for OA = OC $$\Rightarrow \sqrt{{{\left( h-7 \right)}^{2}}+{{\left( k-\left( -1 \right) \right)}^{2}}}=\sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-2 \right)}^{2}}}$$ $$\Rightarrow \sqrt{{{h}^{2}}+{{\left( 7 \right)}^{2}}-2\left( 7 \right)\left( h \right)+{{k}^{2}}+{{1}^{2}}+2\left( k \right)\left( 1 \right)}=\sqrt{{{h}^{2}}+{{1}^{2}}-2\left( h \right)\left( 1 \right)+{{k}^{2}}+{{2}^{2}}-2\left( 2 \right)\left( k \right)}$$ $$\Rightarrow \sqrt{{{h}^{2}}+49-14h+{{k}^{2}}+1+2k}=\sqrt{{{h}^{2}}+{{1}^{2}}-2h\left( 1 \right)+{{k}^{2}}+{{2}^{2}}-2\left( 2 \right)\left( k \right)}$$ On squaring both sides, we get $${{h}^{2}}+{{k}^{2}}-14h+2k+50={{h}^{2}}+{{k}^{2}}-2h-4k+5$$ $$\Rightarrow -14k+2k+50=-2h-4k+5$$ $$\Rightarrow -12h+6k=-45$$ $$\Rightarrow 12h-65=45....\left( vi \right)$$ Now, solving the equations (v) and (vi), we get, $$\begin{aligned} & +6h-12k=-63 \\\ & \underline{12h-6k=45\text{ }}\text{ } \\\ \end{aligned}$$ Multiplying the equation (v) with 2, we get, $$\begin{aligned} & 12h-24k=-126 \\\ & \underline{\begin{aligned} & 12h-6k=45\text{ } \\\ & \text{- + -} \\\ \end{aligned}}\text{ } \\\ & 0-18k=-171\text{ } \\\ \end{aligned}$$ $$k=\dfrac{171}{18}$$ $$k=\dfrac{19}{2}$$ Also, putting the value of $$k=\dfrac{19}{2}$$ in the equation (vi), we get $$12h-6\times \left( \dfrac{19}{2} \right)=45$$ $$\Rightarrow 12h-3\times 19=45$$ $$\Rightarrow 12h-57=45$$ $$\Rightarrow 12h=45+57$$ $$\Rightarrow 12h=102$$ $$\Rightarrow h=\dfrac{102}{12}$$ $$\Rightarrow h=\dfrac{17}{2}$$ So, now we have the coordinates of the center $$\left( h,k \right)$$$$=\left( \dfrac{17}{2},\dfrac{19}{2} \right)$$ Also, we know that OC is the radius of the circle, so from a distance formula, we will calculate the radius of the given circle. We know that the distance formula for $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)$$ is $$OC=\sqrt{{{\left( h-x \right)}^{2}}+{{\left( k-y \right)}^{2}}}$$ Here, $$\left( x,y \right)=\left( 1,2 \right)$$ Coordinates of point C $$OC=\sqrt{{{\left( \dfrac{17}{2}-1 \right)}^{2}}+{{\left( \dfrac{19}{2}-2 \right)}^{2}}}$$ $$OC=\sqrt{\dfrac{{{\left( 15 \right)}^{2}}}{4}+\dfrac{{{\left( 15 \right)}^{2}}}{4}}$$ $$OC=\sqrt{\dfrac{450}{4}}$$ Now, we have all the required values available to form an equation of the circle. We know that the general equation of the circle is: $${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}$$ Putting the values of (h, k) and r in the general equation, we get $$\Rightarrow {{\left( x-\dfrac{17}{2} \right)}^{2}}+{{\left( y-\dfrac{19}{2} \right)}^{2}}={{\left( \sqrt{\dfrac{450}{4}} \right)}^{2}}$$ $$\Rightarrow {{x}^{2}}+{{\left( \dfrac{17}{2} \right)}^{2}}-2\left( \dfrac{17}{2} \right)x+{{y}^{2}}+{{\left( \dfrac{19}{2} \right)}^{2}}-2\left( \dfrac{19}{2} \right)y=\dfrac{450}{4}$$ $$\Rightarrow {{x}^{2}}+{{y}^{2}}-17x-19y+\dfrac{650}{4}=\dfrac{450}{4}$$ $$\Rightarrow {{x}^{2}}+{{y}^{2}}-17x-19y+50=0$$ Thus the equation of the circle is: $${{x}^{2}}+{{y}^{2}}-17x-19y+50=0$$ Note: Alternate method: We can solve this question by directly substituting the values of all the points (vertices of $$\Delta ABC$$) in the general equation of the circle. From the resulting equations, we need to find the coordinates of the center of the circle and constant (h, k) and c. Then by substituting these values of (h, k) and c in the general equation of the circle, we get the required equation of the circle.