Question

Find the equation of the bisector of the angle $A$ of the triangle whose vertices are $A\left( {4,3} \right)$, $B\left( {0,0} \right)$ and $C\left( {2,3} \right)$.

Answer 1

We will first draw the diagram for the corresponding conditions. Let $AM$ be the angle bisector angle $A$. Then, find the coordinates of $M$ using the property of angle bisector and section formula. Then, find the equation of line $AM$ from the coordinates of $A$ and $M$.

Complete step by step solution: We are given that the coordinates of vertices of a triangle are $A\left( {4,3} \right)$, $B\left( {0,0} \right)$ and $C\left( {2,3} \right)$
Let $AM$ be the angle bisector of angle $A$
We will first draw the corresponding figure.

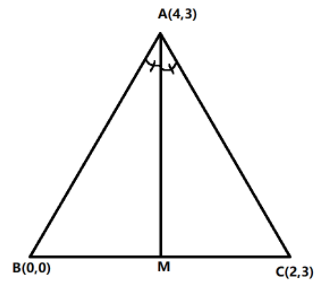
Since $AM$ is an angle bisector, then $AM$ divides the opposite sides of the triangle into two segments which are proportional to the distance of the other two sides.
That is, $AM$ divides $BC$ in the ratio of $AB: AC$
Hence, $AB:AC = AM:MC$
Now, let us find the distance $AB$ and the distance $AC$ using the distance formula,
If $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are coordinates of two points, then distance between them is calculated as $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$AB = \sqrt {{{\left( {4 - 0} \right)}^2} + {{\left( {3 - 0} \right)}^2}} \\\ \Rightarrow AB = \sqrt {16 + 9} \\\ \Rightarrow AB = \sqrt {25} \\\ \Rightarrow AB = 5 \\\$
Similarly the distance of $AC$ is,
$AC = \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( {3 - 3} \right)}^2}} \\\ \Rightarrow AC = \sqrt {4 + 0} \\\ \Rightarrow AC = \sqrt 4 \\\ \Rightarrow AC = 2 \\\$
Thus, the ratio of $AB: AC$ is 5:2 which is also equal to $AM: MC$.
We shall now find the coordinates of $M$ using section formula,
Section formula states that, if $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are coordinates of two points and they are divided by the point $\left( {{x_3},{y_3}} \right)$ in $m:n$,

then the coordinates of $\left( {{x_3},{y_3}} \right)$ are $\left( {{x_3},{y_3}} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$
Therefore, the coordinates of $M$ can be calculated as,
$M = \left( {\dfrac{{\left( 5 \right)2 + \left( 2 \right)0}}{{5 + 2}},\dfrac{{\left( 5 \right)3 + \left( 2 \right)0}}{{5 + 2}}} \right) \\\ M = \left( {\dfrac{{10}}{7},\dfrac{{15}}{7}} \right) \\\$
Next, we will find the equation of line $AM$ using the points $A\left( {4,3} \right)$ and $\left( {\dfrac{{10}}{7},\dfrac{{15}}{7}} \right)$
If $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are coordinates of two points, then the equation of line is given as,
$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
Therefore, equation of $AM$is
$y - \dfrac{{15}}{7} = \dfrac{{3 - \dfrac{{15}}{7}}}{{4 - \dfrac{{10}}{7}}}\left( {x - \dfrac{{10}}{7}} \right) \\\ \Rightarrow y - \dfrac{{15}}{7} = \dfrac{{\dfrac{6}{7}}}{{\dfrac{{18}}{7}}}\left( {x - \dfrac{{10}}{7}} \right) \\\ \Rightarrow y - \dfrac{{15}}{7} = \dfrac{1}{3}\left( {x - \dfrac{{10}}{7}} \right) \\\ \Rightarrow 3y - \dfrac{{45}}{7} = x - \dfrac{{10}}{7} \\\ \Rightarrow 3y - x - \dfrac{{45}}{7} + \dfrac{{10}}{7} = 0 \\\ \Rightarrow 3y - x - \dfrac{{35}}{7} = 0 \\\ \Rightarrow 3y - x - 5 = 0 \\\$
Hence, the equation of the bisector of the angle $A$ of the triangle whose vertices are $A\left( {4,3} \right)$, $B\left( {0,0} \right)$ and $C\left( {2,3} \right)$ is $3y - x - 5 = 0$.

Note: Section formula is used to find the coordinates of the point when the point divides the line joined by two points in a certain ratio. If the point $\left( {{x_3},{y_3}} \right)$ divides the line internally joined by the points, $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$, then the coordinates of the point is given as $\left( {{x_3},{y_3}} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$. But, if the point $\left( {{x_3},{y_3}} \right)$ divides the line externally, then the coordinates of the point is given as $\left( {{x_3},{y_3}} \right) = \left( {\dfrac{{m{x_2} - n{x_1}}}{{m - n}},\dfrac{{m{y_2} - n{y_1}}}{{m - n}}} \right)$