Question

Find the equation of parabola whose focus is $S\left( 1,-7 \right)$ and vertex is $A\left( 1,-2 \right)$

Answer 1

We solve this problem by using the definition of the parabola that is the locus of a point such that Distance from the focus is equal to the perpendicular distance of the point to the directrix. Let us draw the rough figure as follows

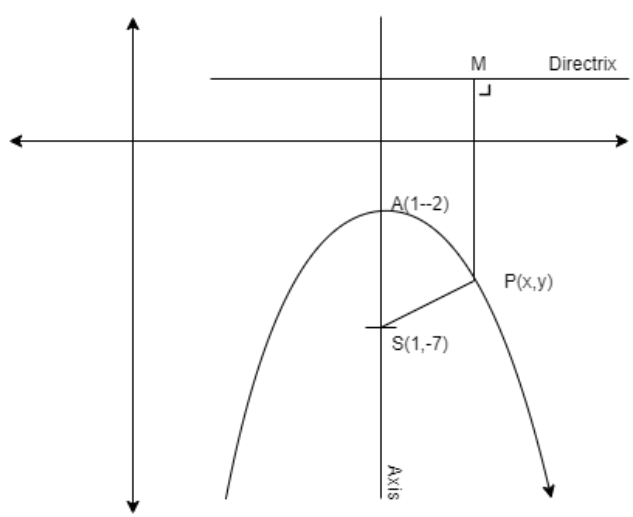
Here the definition of parabola says that
$\Rightarrow SP=PM$
So, for finding the directrix equation consider that the directrix is perpendicular to the axis and point $'A'$ is the midpoint of $'S', 'M'$.

Complete step-by-step solution:
We are given that the focus of parabola is $S\left( 1,-7 \right)$ and vertex is $A\left( 1,-2 \right)$
We know that the point $'A'$ is mid – point of $'S','M\left( h,k \right)'$
We know that if the mid – point of two points $P\left( {{x}_{1}},{{y}_{1}} \right),Q\left( {{x}_{2}},{{y}_{2}} \right)$ is $'R'$ then
$\Rightarrow R=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
By using the above formula to the known condition that $'A'$ is mid – point of $'S','M\left( h,k \right)'$ we get
$\Rightarrow \left( 1,-2 \right)=\left( \dfrac{1+h}{2},\dfrac{-7+k}{2} \right)$
Now by equating the X co – ordinates we get

& \Rightarrow 1=\dfrac{1+h}{2} \\\ & \Rightarrow h=1 \\\ \end{aligned}$$ Now by equating the Y co – ordinates we get $$\begin{aligned} & \Rightarrow -2=\dfrac{-7+k}{2} \\\ & \Rightarrow k=3 \\\ \end{aligned}$$ Therefore the point M is $$\left( 1,3 \right)$$ Now let us find the slope of axis of parabola We have two points on axis of parabola We know that the formula of slope having two points $$P\left( {{x}_{1}},{{y}_{1}} \right),Q\left( {{x}_{2}},{{y}_{2}} \right)$$ is given as $$\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$ By using the above formula to points $$S\left( 1,-7 \right)$$ and $$A\left( 1,-2 \right)$$ we get $$\begin{aligned} & \Rightarrow {{m}_{1}}=\dfrac{-2+7}{1-1} \\\ & \Rightarrow {{m}_{1}}=\dfrac{1}{0} \\\ \end{aligned}$$ We know that the directrix is perpendicular to axis of parabola so, we can say that the slope of directrix is $$\begin{aligned} & \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\\ & \Rightarrow {{m}_{2}}=0 \\\ \end{aligned}$$ We know that the equation of line having one point $$P\left( {{x}_{1}},{{y}_{1}} \right)$$ and slope $$'m'$$ is given as $$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$$ By using the above theorem we can have the equation of directrix as $$\begin{aligned} & \Rightarrow y-3=0\left( x-1 \right) \\\ & \Rightarrow y=3 \\\ \end{aligned}$$ Let us assume that the point ‘P’ as $$\left( x,y \right)$$ We know that the definition of parabola as the locus of point such that Distance from the focus is equal to perpendicular distance of the point to the directrix that is from the figure $$\Rightarrow SP=PM.........equation(i)$$ We know that the distance formula of two points $$P\left( {{x}_{1}},{{y}_{1}} \right),Q\left( {{x}_{2}},{{y}_{2}} \right)$$ as $$\Rightarrow PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$$ We also know that the perpendicular distance of point $$P\left( {{x}_{1}},{{y}_{1}} \right)$$ to the line $$ax+by+c=0$$ is $$\Rightarrow D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$ By using the above two formulas to equation (i) we get $$\Rightarrow \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+7 \right)}^{2}}}=\dfrac{\left| y-3 \right|}{\sqrt{{{0}^{2}}+{{1}^{2}}}}$$ By squaring on both sides we get $$\begin{aligned} & \Rightarrow {{\left( x-1 \right)}^{2}}+{{y}^{2}}+14y+49={{y}^{2}}-6y+9 \\\ & \Rightarrow {{\left( x-1 \right)}^{2}}=-20y-40 \\\ & \Rightarrow {{\left( x-1 \right)}^{2}}=-20\left( y+2 \right) \\\ \end{aligned}$$ Therefore the equation of parabola whose focus is $$S\left( 1,-7 \right)$$ and vertex $$A\left( 1,-2 \right)$$ is $$\Rightarrow {{\left( x-1 \right)}^{2}}=-20\left( y+2 \right)$$ **Note:** We have a shortcut to solve this problem. We know that the general equation of parabola whose axis is parallel to Y-axis but the negative direction is $$\Rightarrow {{x}^{2}}=-4ay............equation(i)$$ Here, $$'a'$$ is the distance between focus and vertex. We know that the distance formula of two points $$P\left( {{x}_{1}},{{y}_{1}} \right),Q\left( {{x}_{2}},{{y}_{2}} \right)$$ as $$\Rightarrow PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$$ By using above formula for focus and vertex we get $$\begin{aligned} & \Rightarrow a=\sqrt{{{\left( 1-1 \right)}^{2}}+{{\left( -2+7 \right)}^{2}}} \\\ & \Rightarrow a=5 \\\ \end{aligned}$$ Here we have the vertex as $$A\left( 1,-2 \right)$$ which means the vertex has been transformed from $$\left( 0,0 \right)$$ to $$\left( 1,-2 \right)$$ By using the transformation of axes to equation (i) we get $$\begin{aligned} & \Rightarrow {{\left( x-1 \right)}^{2}}=-4\times 5\left( y+2 \right) \\\ & \Rightarrow {{\left( x-1 \right)}^{2}}=-20\left( y+2 \right) \\\ \end{aligned}$$ Therefore the equation of parabola whose focus is $$S\left( 1,-7 \right)$$ and vertex $$A\left( 1,-2 \right)$$ is $$\Rightarrow {{\left( x-1 \right)}^{2}}=-20\left( y+2 \right)$$