Question

Find the equation of pair of lines at a distance of 5 units from the line y = 1

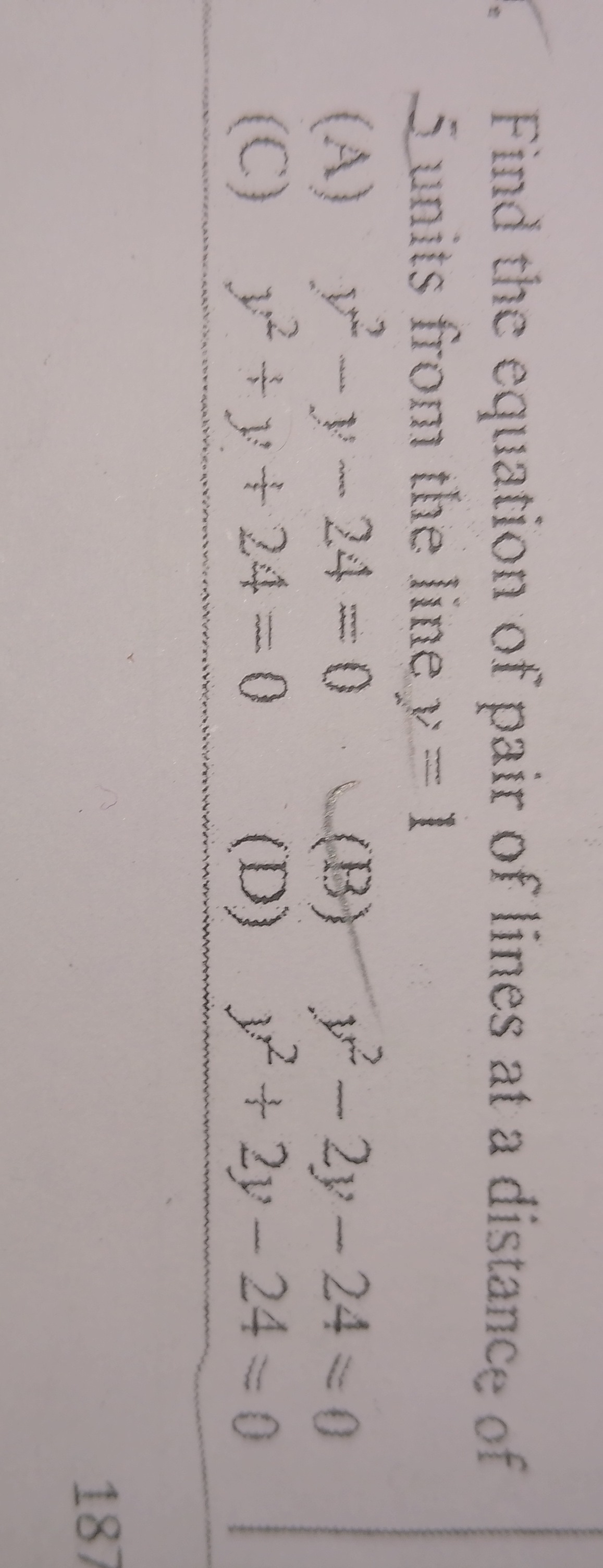
• A. $y^2 - y - 24 = 0$
• B. $y^2 - 2y - 24 = 0$
• C. $y^2 + y + 24 = 0$
• D. $y^2 + 2y - 24 = 0$

Answer 1

Answer: (B)

$y^2 - 2y - 24 = 0$

Answer 2

The given line is $y = 1$. Lines parallel to this line are horizontal and can be written as $y = k$.

The distance between the line $y = k$ and $y = 1$ is given by:

$$|k - 1| = 5$$

Thus, we get:

$$k - 1 = 5 \quad \text{or} \quad k - 1 = -5$$ $$k = 6 \quad \text{or} \quad k = -4$$

So the two lines are:

$$y = 6 \quad \text{and} \quad y = -4$$

To express them as a single equation, we combine:

$$(y - 6)(y + 4) = 0$$

Expanding:

$$y^2 - 6y + 4y - 24 = y^2 - 2y - 24 = 0$$

Thus, the equation of the pair of lines is:

$$y^2 - 2y - 24 = 0$$