Question

Find the equation of line which makes an angle $\alpha$ with x-axis and cut an intercept of length a on it.

Answer 1

Hint: Draw the line on coordinate plane and use equation of line when slope and one point is given i.e. $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$

Complete step-by-step answer:
We have information given from question as
Line makes an angle $\alpha$ with x-axis
Line cuts an intercept of length ‘a’ with x-axis
We know that slope of any line is defined as the tan of angle formed by line with the positive direction of x-axis. Here the angle given is $\alpha$ with the x-axis from point (1).
Hence, the slope of the given line is tan$\alpha$.
Now, coming to the second point; the intercept with x-axis is ‘a’. We already know that the intercept of a line is the length from origin on that axis to the point where the line cuts the axis.
Here, line has intercept of ‘a’ on x-axis, hence we can represent the given line as;

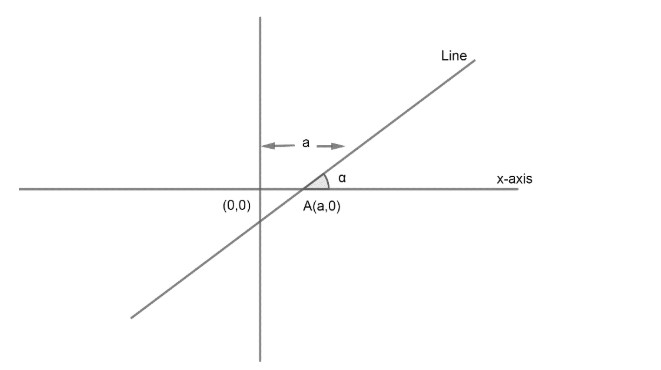
From the given diagram we can write the coordinates of A as (a,0).
As we know that equation of any line can be given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$, if we have a point and slope.
Now, the slope of the line given is tan$\alpha$and one point lying on line is (a,0). So, line can be given by
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Where $\left( {{x}_{1}},{{y}_{1}} \right)=\left( a,0 \right)$ from the diagram
Slope = tan$\alpha$
Hence, line is given by
$\begin{aligned} & y-0=\tan \left( x-a \right) \\\ & y=x\tan \alpha -a\tan \alpha \\\ \end{aligned}$
Writing in the standard form of line i.e. Ax + By + C=0, we can write the equation of line as
$x\tan \alpha -y-a\tan \alpha =0$

Note: One can go wrong with the intercept ‘a’ given. One can take that intercept on y-axis and write the equation of line by y = mx + C, where C is y-intercept and m is slope. Hence the above equation becomes $y=x\tan \alpha +a$ which is wrong as ‘a’ is intercept on x-axis not on y-axis.