Question

Find the equation of line having 3, 4 as intercepts on the coordinate axis
A.4x + 3y = 12
B.4x – 3y = 12
C.3x + 4y = 12
D.3x – 4y =12

Answer 1

Hint: Take the intercepts given as a and b. Substitute these values in the equation of a straight line and simplify it.Match the result with above given options.
Complete step by step answer:
When you have a linear equation, the x – intercept is the point where the graph of the line crosses the x – axis. The y – intercept is the point where the graph of the line crosses the y – axis.
To find the x – intercept of a given linear equation, simplify the ‘y’ and solve for ‘x’. To find the y – intercept, remove the ‘x’ and solve for ‘y’.
The equation of a line which cuts off intercepts a and b respectively from x – axis and y –axis is given by,
$\dfrac{x}{a}+\dfrac{y}{b}=1-(1)$

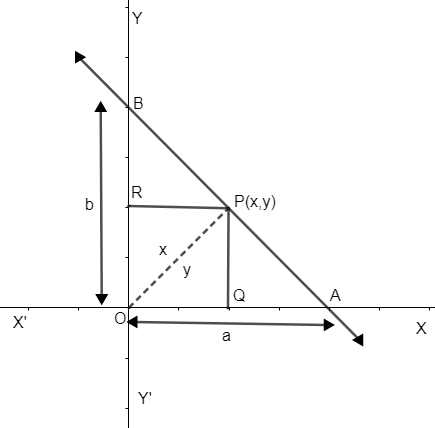
Thus from the figure you can find the intercepts a and b $\dfrac{x}{a}+\dfrac{y}{b}=1$, representing the straight line AB.
We have been given the intercepts as 3 and 4 with the coordinate axis.
Thus a = 3 and b = 4. Now let us substitute this value in equation (1).
$\dfrac{x}{a}+\dfrac{y}{b}=1$
$\Rightarrow \dfrac{x}{3}+\dfrac{y}{4}=1$
Cross multiply and simplify the expression.

& \dfrac{4x+3y}{3\times 4}=1 \\\ & \Rightarrow 4x+3y=12 \\\ \end{aligned}$$ Thus we got the equation of line as 4x + 3y = 12. $$\therefore $$ Option (a) is the correct answer. Note: The straight line $$\dfrac{x}{a}+\dfrac{y}{b}=1$$ in the figure intersects the x – axis at A (a, 0) and the y –axis at B (0, b). The x – intercept and y – intercept i.e. a and b can be positive or negative.