Question

Find the equation of circle if:
(i) centre $\left( a,b \right)$ and radius $\sqrt{{{a}^{2}}+{{b}^{2}}}$ .
(ii) centre $\left( a\sec \alpha ,b\tan \alpha \right)$ and radius $\sqrt{{{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha }$ .

Answer 1

Hint : First, we should know the general form of equation of circle which is given as ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$ where $\left( h,k \right)$ is centre points of circle and r is radius of circle. The, we will substitute value given to us in the above general form and on solving, we will get the required answer. Here, we will be using the formula such as ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ , ${{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1$ .

Complete step-by-step answer :
Here, we know the general form of equation of circle which is given as ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$ where $\left( h,k \right)$ is centre points of circle and r is radius of circle.
So, we will substitute the values given to us in general form and will get the answer.
Taking case(i): centre $\left( a,b \right)$ and radius $\sqrt{{{a}^{2}}+{{b}^{2}}}$ . In place of $\left( h,k \right)$ we will put $\left( a,b \right)$ and in place of r, $\sqrt{{{a}^{2}}+{{b}^{2}}}$ .

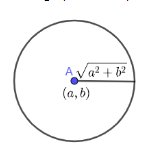
So, we will get equation as
${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{\left( \sqrt{{{a}^{2}}+{{b}^{2}}} \right)}^{2}}$
On using the formula ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ , we will expand the equation. We will get as
${{x}^{2}}+{{a}^{2}}-2xa+{{y}^{2}}+{{b}^{2}}-2yb={{a}^{2}}+{{b}^{2}}$
On further solving and taking all the terms on left-hand side, we get as
${{x}^{2}}+{{a}^{2}}-2xa+{{y}^{2}}+{{b}^{2}}-2yb-{{a}^{2}}-{{b}^{2}}=0$
We will cancel the positive negative terms and will get as
${{x}^{2}}-2xa+{{y}^{2}}-2yb=0$
On rearranging the terms, we will get final equation as
${{x}^{2}}+{{y}^{2}}-2xa-2yb=0$ ……………………………….(1)
Taking case (ii): centre $\left( a\sec \alpha ,b\tan \alpha \right)$ and radius $\sqrt{{{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha }$ . In place of $\left( h,k \right)$ we will put $\left( a\sec \alpha ,b\tan \alpha \right)$ and in place of r, $\sqrt{{{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha }$ .

So, we will get equation as
${{\left( x-a\sec \alpha \right)}^{2}}+{{\left( y-b\tan \alpha \right)}^{2}}={{\left( \sqrt{{{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha } \right)}^{2}}$
On using the formula ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ , we will expand the equation. We will get as
${{x}^{2}}+{{a}^{2}}{{\sec }^{2}}\alpha -2xa\sec \alpha +{{y}^{2}}+{{b}^{2}}{{\tan }^{2}}\alpha -2yb\tan \alpha ={{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha$
Now, we will use the identity ${{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1$ and by using this we will get equation as
${{x}^{2}}+{{a}^{2}}{{\sec }^{2}}\alpha -2xa\sec \alpha +{{y}^{2}}+{{b}^{2}}\left( {{\sec }^{2}}\alpha -1 \right)-2yb\tan \alpha ={{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha$
On further solving, we will get as
${{x}^{2}}+{{a}^{2}}{{\sec }^{2}}\alpha -2xa\sec \alpha +{{y}^{2}}+{{b}^{2}}{{\sec }^{2}}\alpha -b-2yb\tan \alpha ={{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha$
Taking all the terms on left hand side and on cancelling positive negative terms we will get equation as
${{x}^{2}}+{{a}^{2}}{{\sec }^{2}}\alpha -2xa\sec \alpha +{{y}^{2}}+{{b}^{2}}{{\sec }^{2}}\theta -b-2yb\tan \alpha -{{a}^{2}}{{\sec }^{2}}\alpha -{{b}^{2}}{{\sec }^{2}}\alpha =0$
${{x}^{2}}-2xa\sec \alpha +{{y}^{2}}-b-2yb\tan \alpha =0$
Taking constant term b to right hand side, and on rearranging the terms we get as
${{x}^{2}}+{{y}^{2}}-2xa\sec \alpha -2yb\tan \alpha -b=0$ ……………………………(2)
Thus, equation of circle with centre $\left( a,b \right)$ and radius $\sqrt{{{a}^{2}}+{{b}^{2}}}$ is ${{x}^{2}}+{{y}^{2}}-2xa-2yb=0$ and with centre $\left( a\sec \alpha ,b\tan \alpha \right)$ and radius $\sqrt{{{a}^{2}}{{\sec }^{2}}\alpha +{{b}^{2}}{{\sec }^{2}}\alpha }$ is ${{x}^{2}}+{{y}^{2}}-2xa\sec \alpha -2yb\tan \alpha -b=0$ .

Note : Students should know the general form of the circle equation while solving then only the correct answer will be obtained. Also, the general form after solving we always be in form of ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ so, from this also we can compare or obtained answer whether it is in correct form or not.