Question

Find the equation of a straight line passing through $\left( 1,-4 \right)$ and have intercepts which are in the ratio $2:5$ .

Answer 1

First we will take a common ratio then we will get the intercepts as 2t and 5t , then we will put these values in general equation of line in intercept form that is $\dfrac{x}{a}+\dfrac{y}{b}=1$ and then we will put the point $\left( 1,-4 \right)$in this equation and get the value of t and eventually get the equation of line.

Complete step by step answer:
We are given that the line passes through a point that is $\left( 1,-4 \right)$ and it is given that the intercept is in the ratio: $2:5$.
Now, let the common ratio be t , since the intercepts are in the ratio $2:5$ , therefore the intercept on x-axis will be 2t and the intercept on the y-axis will be 5t,
Now, we know that the general equation of line in intercept form is as follows:
$\dfrac{x}{a}+\dfrac{y}{b}=1$ , where a and b are the intercept of the given line.
Now, we will put the intercepts given in the question that are 2t and 5t, therefore we will get:
$\dfrac{x}{2t}+\dfrac{y}{5t}=1\text{ }.........\left( 1 \right)$
Now, it is given that the line passes through $\left( 1,-4 \right)$ , therefore we will put these coordinates in the given line:
$\dfrac{1}{2t}+\dfrac{-4}{5t}=1$
We will now solve this equation to get the value of t : $\dfrac{5-8}{10t}=1$ , we will now take 10t on the right hand side, therefore we will get: $-3=10t\Rightarrow t=\dfrac{-3}{10}$
We will put the value of t in equation 1 , therefore we will get:
$\Rightarrow \dfrac{x}{2\left( \dfrac{-3}{10} \right)}+\dfrac{y}{5\left( \dfrac{-3}{10} \right)}=1\Rightarrow \dfrac{x}{\left( \dfrac{-3}{5} \right)}+\dfrac{y}{\left( \dfrac{-3}{2} \right)}=1\Rightarrow \dfrac{5x}{-3}+\dfrac{2y}{-3}=1$

Now, we will take 3 on the right hand side, therefore we will get: $5x+2y=-3\Rightarrow 5x+2y+3=0$ .

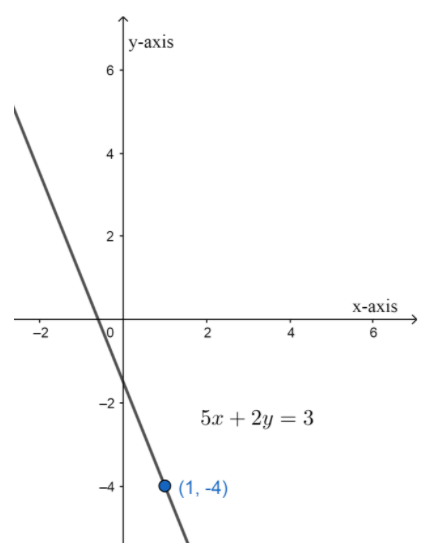
Hence, the equation of the line is: $5x+2y+3=0$

Note: Student can make a silly mistake while putting the values of coordinates in equation 1 like we have $\left( 1,-4 \right)$ , and if we make the mistake of putting $\left( -1,4 \right)$ in equation 1 then whole answer will change and eventually we will get: $5x+2y-3=0$ which is not the correct answer.