Question
Question: Find the equation of a circle which passes through \(\left( 4,1 \right),\left( 6,5 \right)\) and has...
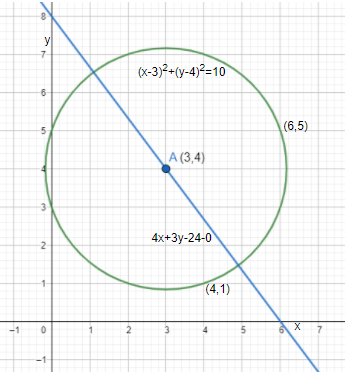
Find the equation of a circle which passes through (4,1),(6,5) and has the center on: 4x+3y−24=0.
Solution
In this question we have been given with the coordinates of the points on a circle and an equation of a line which passes through the center of the circle. We know that the equation of a circle with center (h,k) is (x−h)2+(y−k)2=r2. Given the points lie on the circle, we will use the distance formula which is given by (x1−x2)2+(y1−y2)2 equate the two distances to find the value of h and k. We will then substitute the values in the equation of the circle and get the required solution.
Complete step by step solution:
Since the center of the circle lies on the line 4x+3y−24=0
Therefore, we can write:
4x+3y−24=0→(1)
Now given the points (4,1),(6,5) lie on the circle. The distance of these points from the center of the circle will be same. Therefore, we can equate the distance of both the points from the circle.
The distance from (4,1) to (h,k) will be: (4−h)2+(1−k)2
The distance from (6,5) to (h,k) will be: (6−h)2+(5−k)2
Since the distance is the same, we can write:
⇒(4−h)2+(1−k)2=(6−h)2+(5−k)2
On using the expansion formula, we get:
⇒16+h2−8h+1+k2−2k=36−h2−12h+25+k2−10k
On simplifying the terms, we get:
⇒h2+k2−8h−2k+17=h2+k2−12h−10k+61
On squaring both sides, we get:
⇒h2+k2−8h−2k+17=h2+k2−12h−10k+61
On cancelling the similar terms, we get:
⇒8h+2k−17=12h+10k−61
On simplifying, we get:
⇒4h+8k−44=0→(2)
On subtracting equation (1) from (2), we get:
⇒5k−20=0
On rearranging and simplifying, we get:
⇒k=4
On substituting k=4 in equation (2), we get:
⇒4h+8(4)−44=0→(2)
On simplifying, we get:
⇒h=312
On dividing, we get:
⇒h=3
Thus, the center of the circle (h,k) is (3,4)
Now the radius of the circle is r=(x−h)2+(y−k)2
On substituting the values, we get:
⇒r=(4−3)2+(1−4)2
On simplifying the roots, we get:
⇒r=1+9
Which can be simplified as:
r=10
On substituting the values in the equation of the circle, we get:
⇒(x−3)2+(y−4)2=10, which is the required solution.
On drawing the line and the circle on the graph, we get:
Note: The most common way of making a mistake is not applying the distance formula and the general equation of the circle correctly. It is to be remembered that the entire premise of solving the question is remembering that points on a circle are always equidistant from the center of the circle.
