Question

Find the equation and the length of the common chord of the two circles whose equations are ${x^2} + {y^2} + 3x + 5y + 4 = 0$ and ${x^2} + {y^2} + 5x + 3y + 4 = 0$.

Answer 1

Hint- Here, we will proceed by subtracting the given equations of the two circles in order to obtain the equation of the common chord between these two circles. Then, we will use the formula ${\text{L}} = \dfrac{{2{{\text{R}}_1}{{\text{R}}_2}}}{d}$ in order to find the length of the common chord.

Complete step-by-step answer:

Given equations of the two circles are ${x^2} + {y^2} + 3x + 5y + 4 = 0{\text{ }} \to {\text{(1)}}$ and ${x^2} + {y^2} + 5x + 3y + 4 = 0{\text{ }} \to {\text{(2)}}$
As we know that the equation of the common chord between any two circles can be obtained by subtracting the equations of the two circles.
By subtracting equation (2) from equation (1), we get
$\Rightarrow {x^2} + {y^2} + 3x + 5y + 4 - \left( {{x^2} + {y^2} + 5x + 3y + 4} \right) = 0 - 0 \\\ \Rightarrow {x^2} + {y^2} + 3x + 5y + 4 - {x^2} - {y^2} - 5x - 3y - 4 = 0 \\\ \Rightarrow - 2x + 2y = 0 \\\ \Rightarrow - x + y = 0 \\\ \Rightarrow x = y \\\$
Therefore, the required equation of the common chord of the two given circles is x = y.
Since, the general form of the equation of any circle having centre as C(a,b) and radius as r can be represented as ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}{\text{ }} \to {\text{(3)}}$
Using completing the square method, the given equations of the circle can be rewritten in the same form as given by equation (3).
Rewriting equation (1) in the same form as given by equation (3), we have
$\Rightarrow {x^2} + 3x + {\left( {\dfrac{3}{2}} \right)^2} - {\left( {\dfrac{3}{2}} \right)^2} + {y^2} + 5y + {\left( {\dfrac{5}{2}} \right)^2} - {\left( {\dfrac{5}{2}} \right)^2} + 4 = 0 \\\ \Rightarrow \left[ {{x^2} + 2\left( {\dfrac{3}{2}} \right)\left( x \right) + {{\left( {\dfrac{3}{2}} \right)}^2}} \right] + \left[ {{y^2} + 2\left( {\dfrac{5}{2}} \right)\left( y \right) + {{\left( {\dfrac{5}{2}} \right)}^2}} \right] = {\left( {\dfrac{3}{2}} \right)^2} + {\left( {\dfrac{5}{2}} \right)^2} - 4 \\\ \Rightarrow \left[ {{{\left( {x + \dfrac{3}{2}} \right)}^2}} \right] + \left[ {{{\left( {y + \dfrac{5}{2}} \right)}^2}} \right] = \dfrac{9}{4} + \dfrac{{25}}{4} - 4 \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{3}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{5}{2}} \right)} \right]^2} = \dfrac{{9 + 25 - 16}}{4} \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{3}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{5}{2}} \right)} \right]^2} = \dfrac{{18}}{4} \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{3}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{5}{2}} \right)} \right]^2} = \dfrac{9}{2} \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{3}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{5}{2}} \right)} \right]^2} = {\left( {\dfrac{3}{{\sqrt 2 }}} \right)^2}{\text{ }} \to {\text{(4)}} \\\$
By comparing equations (3) and (4), we get
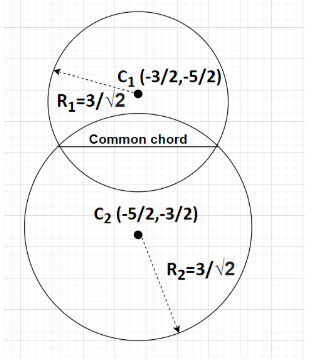
So, the centre of the circle ${x^2} + {y^2} + 3x + 5y + 4 = 0$ is ${{\text{C}}_1}\left( { - \dfrac{3}{2}, - \dfrac{5}{2}} \right)$ and radius is ${{\text{R}}_1} = \dfrac{3}{{\sqrt 2 }}$
Rewriting equation (2) in the same form as given by equation (3), we have
$\Rightarrow {x^2} + 5x + {\left( {\dfrac{5}{2}} \right)^2} - {\left( {\dfrac{5}{2}} \right)^2} + {y^2} + 3y + {\left( {\dfrac{3}{2}} \right)^2} - {\left( {\dfrac{3}{2}} \right)^2} + 4 = 0 \\\ \Rightarrow \left[ {{x^2} + 2\left( {\dfrac{5}{2}} \right)\left( x \right) + {{\left( {\dfrac{5}{2}} \right)}^2}} \right] + \left[ {{y^2} + 2\left( {\dfrac{3}{2}} \right)\left( y \right) + {{\left( {\dfrac{3}{2}} \right)}^2}} \right] = {\left( {\dfrac{5}{2}} \right)^2} + {\left( {\dfrac{3}{2}} \right)^2} - 4 \\\ \Rightarrow \left[ {{{\left( {x + \dfrac{5}{2}} \right)}^2}} \right] + \left[ {{{\left( {y + \dfrac{3}{2}} \right)}^2}} \right] = \dfrac{{25}}{4} + \dfrac{9}{4} - 4 \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{5}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{3}{2}} \right)} \right]^2} = \dfrac{{25 + 9 - 16}}{4} \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{5}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{3}{2}} \right)} \right]^2} = \dfrac{{18}}{4} \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{5}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{3}{2}} \right)} \right]^2} = \dfrac{9}{2} \\\ \Rightarrow {\left[ {x - \left( { - \dfrac{5}{2}} \right)} \right]^2} + {\left[ {y - \left( { - \dfrac{3}{2}} \right)} \right]^2} = {\left( {\dfrac{3}{{\sqrt 2 }}} \right)^2}{\text{ }} \to {\text{(5)}} \\\$
By comparing equations (3) and (5), we get
So, the centre of the circle ${x^2} + {y^2} + 5x + 3y + 4 = 0$ is ${{\text{C}}_2}\left( { - \dfrac{5}{2}, - \dfrac{3}{2}} \right)$ and radius is ${{\text{R}}_2} = \dfrac{3}{{\sqrt 2 }}$
According to the distance formula, the distance between any two points A(a,b) and B(c,d) is given by
$d = \sqrt {{{\left( {c - a} \right)}^2} + {{\left( {d - b} \right)}^2}}$
Using the above formula, the distance between the centres of the two circles i.e.,${{\text{C}}_1}\left( { - \dfrac{3}{2}, - \dfrac{5}{2}} \right)$ and ${{\text{C}}_2}\left( { - \dfrac{5}{2}, - \dfrac{3}{2}} \right)$ is given by

$$\Rightarrow d = \sqrt {{{\left[ { - \dfrac{5}{2} - \left( { - \dfrac{3}{2}} \right)} \right]}^2} + {{\left[ { - \dfrac{3}{2} - \left( { - \dfrac{5}{2}} \right)} \right]}^2}} \\\ \Rightarrow d = \sqrt {{{\left[ { - \dfrac{5}{2} + \dfrac{3}{2}} \right]}^2} + {{\left[ { - \dfrac{3}{2} + \dfrac{5}{2}} \right]}^2}} \\\ \Rightarrow d = \sqrt {{{\left[ {\dfrac{{ - 5 + 3}}{2}} \right]}^2} + {{\left[ {\dfrac{{ - 3 + 5}}{2}} \right]}^2}} \\\ \Rightarrow d = \sqrt {{{\left[ {\dfrac{{ - 2}}{2}} \right]}^2} + {{\left[ {\dfrac{2}{2}} \right]}^2}} \\\ \Rightarrow d = \sqrt {{{\left[ { - 1} \right]}^2} + {{\left[ 1 \right]}^2}} \\\ \Rightarrow d = \sqrt {1 + 1} \\\ \Rightarrow d = \sqrt 2 \\\$$

Also, the length of the common tangent between two circles having radii as ${{\text{R}}_1}$ and ${{\text{R}}_2}$ is given by
${\text{L}} = \dfrac{{2{{\text{R}}_1}{{\text{R}}_2}}}{d}{\text{ }} \to {\text{(6)}}$ where d is the distance between the centres of the two given circles.
By putting ${{\text{R}}_1} = \dfrac{3}{{\sqrt 2 }}$, ${{\text{R}}_2} = \dfrac{3}{{\sqrt 2 }}$ and $d = \sqrt 2$ in equation (6), we get

$$\Rightarrow {\text{L}} = \dfrac{{2\left( {\dfrac{3}{{\sqrt 2 }}} \right)\left( {\dfrac{3}{{\sqrt 2 }}} \right)}}{{\sqrt 2 }} \\\ \Rightarrow {\text{L}} = \dfrac{{2\left( {\dfrac{9}{2}} \right)}}{{\sqrt 2 }} \\\ \Rightarrow {\text{L}} = \dfrac{9}{{\sqrt 2 }} \\\$$

Therefore, the required length of the common chord of the two given circles is $\dfrac{9}{{\sqrt 2 }}$.

Note- In this particular problem, we have converted the equations of the given two circles in the same form of the equation of any circle which is ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$ in order to find the centre coordinates of both the circles and their radii which can further be utilized to get the value of the distance between the centres of these circles.