Question

Find the envelope of a straight line which moves so that the sum of squares of the perpendicular drawn to it from two given points is constant.

Answer 1

Hint : First of all write the parametric equation of a straight line which involves distance of the line from the origin so origin becomes one of the points which is at a perpendicular distance from the straight line so let us assume the parametric equation of a straight line as $x\cos \theta +y\sin \theta =p$ where p is the perpendicular distance from origin of the Cartesian coordinates and $\theta$ is the angle made by that line segment having length p from x axis. Then assume the other point $A\left( a,0 \right)$ and write the perpendicular distance of this point from the straight line. Now, square the distances from origin and from point A and add them and equate it to some constant “c”. Then arrange the equations in such a way that we will get the relation between x and y which will be the envelope.

Complete step-by-step answer :
First of all we are going to write the equation of a straight line in a parametric form:
$x\cos \theta +y\sin \theta =p$
In the above equation, p represents the perpendicular distance from origin to the straight line and $\theta$ is the angle that the line segment with length p made by x axis in the Cartesian plane.
In the below figure, we are demonstrating the straight line that we have written above:

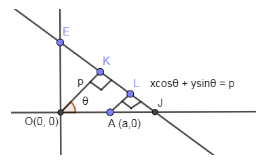
In the above diagram, the two given points in the question from where the perpendicular lines are drawn is point O and point A. OK and AL are the perpendicular distances from the given points O and A.
Now, the perpendicular distance from O to the straight line is “p” and the perpendicular distance from the other given point $A\left( a,0 \right)$ is calculated as follows:
We know that, the perpendicular distance from a point $P\left( {{x}_{1}},{{y}_{1}} \right)$ from the line $ax+by+c=0$ is calculated by using the following formula:
$\dfrac{\left| a\left( {{x}_{1}} \right)+b\left( {{y}_{1}} \right)+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
Applying this formula to find the perpendicular distance from point $A\left( a,0 \right)$ to the straight line $x\cos \theta +y\sin \theta =p$ we get,
$\dfrac{\left| a\cos \theta -p \right|}{\sqrt{{{\cos }^{2}}\theta +{{\sin }^{2}}\theta }}$
From the trigonometric identity, the value of ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$ so substituting this value in the above expression we get,
$\dfrac{\left| a\cos \theta -p \right|}{1}$
Now, squaring the distances p and $a\cos \theta -p$ we get,
$\begin{aligned} & {{p}^{2}}+{{\left( a\cos \theta -p \right)}^{2}} \\\ & ={{p}^{2}}+{{a}^{2}}{{\cos }^{2}}\theta +{{p}^{2}}-2ap\cos \theta \\\ & =2{{p}^{2}}+{{a}^{2}}{{\cos }^{2}}\theta -2ap\cos \theta \\\ \end{aligned}$
Now, it is given that the sum of the squares of the distances from given points is a constant so the above expression will be constant when the expression ${{a}^{2}}{{\cos }^{2}}\theta -2ap\cos \theta$ becomes 0 because it has a variable $\theta$ in it.
So, equating ${{a}^{2}}{{\cos }^{2}}\theta -2ap\cos \theta$ to 0 we get,
${{a}^{2}}{{\cos }^{2}}\theta -2ap\cos \theta =0$
Taking $\cos \theta$ as common in the above equation we get,
$\cos \theta \left( a\cos \theta -2ap \right)=0$
Equating $a\cos \theta -2ap$ to 0 we get,
$a\cos \theta -2ap=0$
$\begin{aligned} & \Rightarrow \cos \theta =\dfrac{2ap}{a} \\\ & \Rightarrow \cos \theta =2p \\\ \end{aligned}$
We can find the $\sin \theta$ by using the trigonometric identity:
$\begin{aligned} & {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\\ & \Rightarrow {{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \\\ & \Rightarrow \sin \theta =\sqrt{1-{{\cos }^{2}}\theta } \\\ \end{aligned}$
Substituting $\cos \theta =2p$ in the above equation we get,
$\sin \theta =\sqrt{1-4{{p}^{2}}}$
The straight line equation that we have shown above is:
$x\cos \theta +y\sin \theta =p$
Subtracting $x\cos \theta$ on both the sides of the above equation we get,
$y\sin \theta =p-x\cos \theta$
Substituting the value of $\cos \theta \And \sin \theta$ that we have derived above we get,
$y\sqrt{1-4{{p}^{2}}}=p-x\left( 2p \right)$
Squaring on both the sides of the above equation we get,
$\begin{aligned} & {{y}^{2}}\left( 1-4{{p}^{2}} \right)={{p}^{2}}{{\left( 1-2x \right)}^{2}} \\\ & \Rightarrow {{y}^{2}}\left( 1-4{{p}^{2}} \right)={{p}^{2}}\left( 1+4{{x}^{2}}-4x \right) \\\ \end{aligned}$
Rearranging the above equation we get,
$4{{p}^{2}}{{x}^{2}}+\left( 4{{p}^{2}}-1 \right){{y}^{2}}-4{{p}^{2}}x+{{p}^{2}}=0$
The above equation is representing the central conic and the above equation is also the envelope of a straight line which moves so that the sum of squares of the perpendicular drawn to it from two given points is constant.
Hence, the required envelope is the central conic.

Note : A trick to remember to solve these type of questions in which we have to find the envelope that is restricted by some conditions is you have to find the relation between x and y which you can see from the solution that first of all we write the equation with some variable $\theta$ then we apply the conditions given in the question and by arrangement of equations we have eliminated the variable $\theta$ and ultimately we have found the relation between x and y.
So, whenever in the question you will see the words like “envelope or locus” then basically in mathematical terms you have to find the relation between x and y.