Question

Find the entire length of the cardioid $r=a\left( 1+\cos \theta \right)$. Also, show that the upper half is bisected by $\theta =\dfrac{\pi }{3}$.

Answer 1

First, by using the formula of the length(L) of the cardioids is given by $L=2\int\limits_{0}^{\pi }{\sqrt{\left( {{r}^{2}}+{{\left( \dfrac{dr}{d\theta } \right)}^{2}} \right)}d\theta }$. Then, to get the length L of the cardioids, we need to solve the above expression by substituting the value of r and $\dfrac{dr}{d\theta }$. Then, by using some of the basic properties of the trigonometric functions, we get the length of the upper half and its bisection angle also.

Complete step-by-step solution:
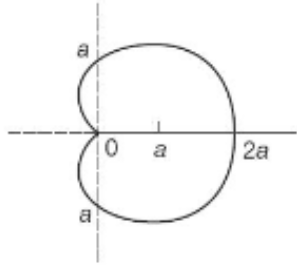
In this question, we are supposed to find the entire length of the cardioid $r=a\left( 1+\cos \theta \right)$.
So, before proceeding for this, we must know that the cardioids is symmetrical about the initial line, and for its upper half, $\theta$ goes on increasing from 0 to $\pi$.

So, it gives rise to the following condition by differentiating the given cardioids function as:
$\begin{aligned} & \dfrac{dr}{d\theta }=\dfrac{d}{d\theta }a\left( 1+\cos \theta \right) \\\ & \Rightarrow \dfrac{dr}{d\theta }=-a\sin \theta \\\ \end{aligned}$
Now, by using the formula of the length(L) of the cardioids which is given by:
$L=2\int\limits_{0}^{\pi }{\sqrt{\left( {{r}^{2}}+{{\left( \dfrac{dr}{d\theta } \right)}^{2}} \right)}d\theta }$
Now, to get the length L of the cardioids, we need to solve the above expression by substituting the value of r and $\dfrac{dr}{d\theta }$ in the above function as:
$\begin{aligned} & L=2\int\limits_{0}^{\pi }{\sqrt{\left( {{\left[ a\left( 1+\cos \theta \right) \right]}^{2}}+{{\left( -a\sin \theta \right)}^{2}} \right)}d\theta } \\\ & \Rightarrow L=2a\int\limits_{0}^{\pi }{\sqrt{\left( 1+{{\cos }^{2}}\theta +2\cos \theta +{{\sin }^{2}}\theta \right)}d\theta } \\\ \end{aligned}$
Now, by using the basic formulas of the trigonometry that states us with the fact as:
${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$
Then, by using this trigonometric formula, we get the above integral as:
$L=2a\int\limits_{0}^{\pi }{\sqrt{\left( 2+2\cos \theta \right)}d\theta }$
Then, again by using another trigonometric formula as:
$1+\cos \theta =2{{\cos }^{2}}\dfrac{\theta }{2}$
Then, by using this trigonometric formula, we get the above integral as:

& L=2a\int\limits_{0}^{\pi }{\sqrt{2\times 2{{\cos }^{2}}\dfrac{\theta }{2}}d\theta } \\\ & \Rightarrow L=4a\int\limits_{0}^{\pi }{\cos \dfrac{\theta }{2}d\theta } \\\ & \Rightarrow L=4a\left| \dfrac{\sin \dfrac{\theta }{2}}{\dfrac{1}{2}} \right|_{0}^{\pi } \\\ & \Rightarrow L=8a\left( \sin \dfrac{\pi }{2}-\sin 0 \right) \\\ & \Rightarrow L=8a \\\ \end{aligned}$$ So, the length of the cardioids is 8a. Now, by dividing the entire length of the cardioids by 2, we get the value of the length of the upper half of the curve is 4a. Then, we are asked to show that the upper half of the cardioid is bisected by $\theta =\dfrac{\pi }{3}$ which gives the range from 0 to $\dfrac{\pi }{3}$. Now, by substituting the range of the integral from 0 to $\dfrac{\pi }{3}$ to prove the given fact. So, the required integral is as: $$\begin{aligned} & \int\limits_{0}^{\dfrac{\pi }{3}}{\sqrt{2\left( 1+\cos \theta \right)}d\theta =2a}\int\limits_{0}^{\dfrac{\pi }{3}}{\cos \dfrac{\theta }{2}}d\theta \\\ & \Rightarrow 4a\left| \sin \dfrac{\theta }{2} \right|_{0}^{\dfrac{\pi }{3}} \\\ & \Rightarrow 4a\left( \sin \dfrac{\pi }{6}-\sin 0 \right) \\\ & \Rightarrow 4a\times \dfrac{1}{2} \\\ & \Rightarrow 2a \\\ \end{aligned}$$ **So, the upper half is bisected by $\theta =\dfrac{\pi }{3}$ which gives the length of the upper half as 2a. Hence, the length of the upper half of the curve is 4a and it is bisected by $\theta =\dfrac{\pi }{3}$.** **Note:** Now, to solve these type of the questions we need to know some of the basic trigonometric properties so that these type of questions can be solved easily. Then, some of the basic trigonometric properties are: $\begin{aligned} & {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\\ & 1+\cos \theta =2{{\cos }^{2}}\dfrac{\theta }{2} \\\ \end{aligned}$.