Question
Question: Find the emf \(\left( V \right)\) and internal resistance \(\left( r \right)\) of a single battery w...
Find the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emfs V1 and V2 and internal resistance r1 and r2 respectively, with polarities as shown in the figure.
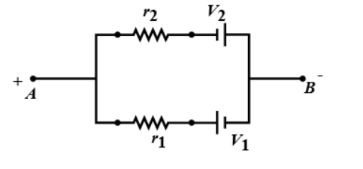
Solution
You can easily solve the question by using the formula which gives the net emf and resistances when two or more batteries are in parallel arrangement. The formula is given as:
Veq=req1∑riVi and the net resistance (req) is found out by using the generic relation of resistances in parallel arrangement.
Complete step by step answer:
We will try to solve the question through the approach described in the hint section of the solution to the question. We will first find the net resistance as it is easier to find out since the formula is very basic and generic and also needed to find the net emf. Then, we will use the formula mentioned above to find the net emf when multiple batteries are connected in parallel combination.
So, let’s first find the net resistance:
We already know that when resistors are in parallel combination, we can write:
req1=∑ri1
Using this here, we get:
req1=r11+r21
After solving and reciprocating, we get:
req=r1+r2r1r2
Now, let’s find the value of net emf in the given arrangement:
First, let us write the formula that we will use:
Veq=req1∑riVi
We can write it as following, in our case:
Veq=req1r1V1+(r2−V2)
After solving this and simplifying, we get:
Veq=r1+r2V1r2−V2r1
Hence, we get the net emf as, Veq=r1+r2V1r2−V2r1
And the net resistance as, req=r1+r2r1r2
Note: Always remember the formula of net emf when cells or batteries are in parallel arrangement as this is very frequently used and thus, helps in the long term. Many students make mistakes in the given question as they forget to include the negative sign in the formula since V2 is of opposite polarity and thus, has a negative effect.
