Question

Find the electric potential at the axis of a uniformly charged disc and use the potential to find the electric field at the same point.

Answer 1

First consider a small part of that disc that has a radius $dr$. We know the equation for electric potential is $V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r}$, so using this equation for that small part of the disc we get the equation $dV = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{dq}}{{\sqrt {{r^2} + {x^2}} }}$. Then integrate this equation and we get this equation $V = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\sqrt {{R^2} + {x^2}} - x} \right]$. We know that the magnitude of the electric field is $E = - \dfrac{{dV}}{{dx}}$, then substitute the value of $V$ in this equation to get this equation $E = - \dfrac{{d\left( {\dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\sqrt {{R^2} + {x^2}} - x} \right]} \right)}}{{dx}}$. Finally, solve this equation to reach the solution.

Complete answer:
Electric field – It is the space around a charge where the electrostatic force of attraction or repulsion can be felt by other charges and charged bodies.
Electric potential –Electric potential at any point is the work done in bringing a unit positive charge in an electric point to that point.

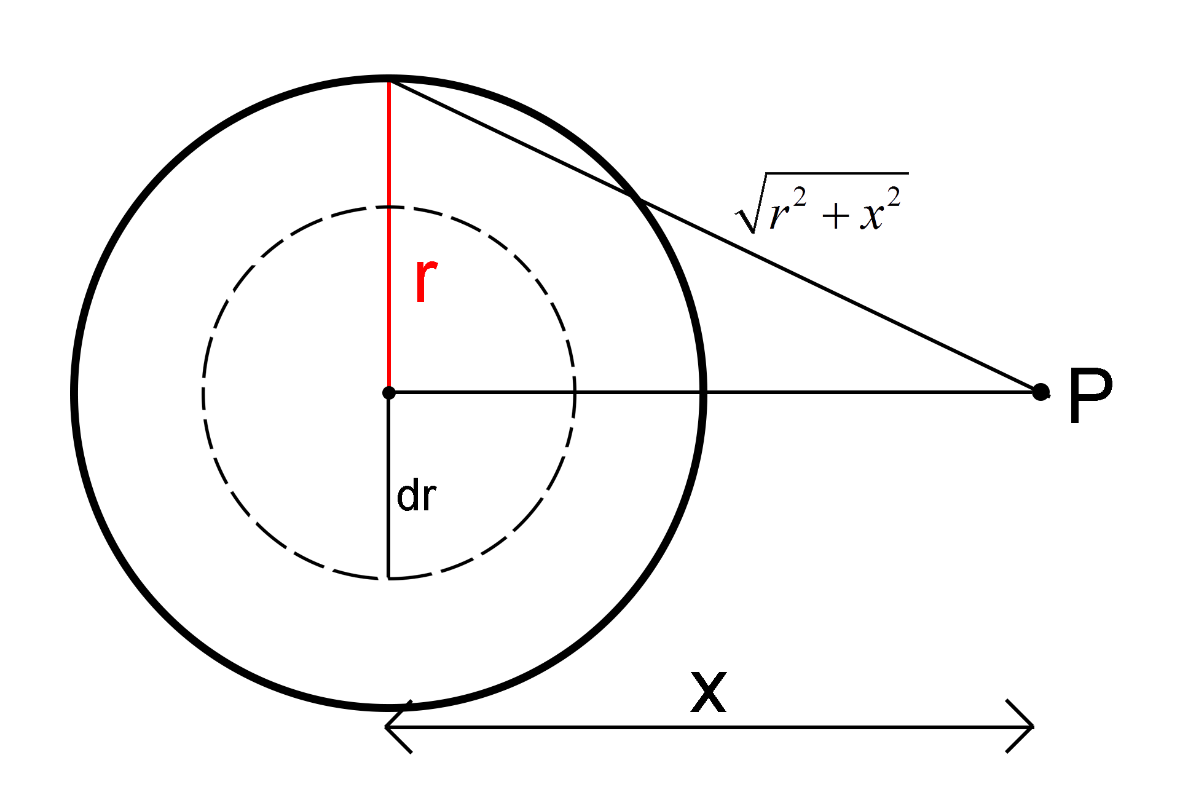
Let’s consider a charged disc of a radius $r$ with a surface charge density $\sigma$. Now let’s consider a point P from the center of the charged disc that is at a distance $x$ from the center of the disc.
To calculate the electric potential at point P due to the charged disc, consider a small part of the disc which is of a radius $dr$.
So, the charge $dq$ of the smaller disc of a radius $dr$ is
$dq =$ The surface charge density of the disc $\times$ Area of the smaller disc
$dq = \sigma \left( {2\pi rdr} \right)$
We know the electric potential at a point is given by
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r}$
Here, $V =$ The electric potential at that point
${\varepsilon _0} =$ The permittivity of free space
$q =$ The magnitude of the charge
$r =$ The distance between the charge and the point
So, the electric point at point P due to the charged disc of a radius $dr$ is
$dV = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{dq}}{{\sqrt {{r^2} + {x^2}} }}$
$\Rightarrow dV = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{\sigma \left( {2\pi rdr} \right)}}{{\sqrt {{r^2} + {x^2}} }}$
Integrating the equation, we get
$\Rightarrow \int\limits_0^R {dV} = \int\limits_0^R {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{\sigma \left( {2\pi rdr} \right)}}{{\sqrt {{r^2} + {x^2}} }}}$
$\Rightarrow \int\limits_0^R {dV} = \dfrac{{2\sigma \pi }}{{4\pi {\varepsilon _0}}}\int\limits_0^R {\dfrac{{rdr}}{{\sqrt {{r^2} + {x^2}} }}}$
$\Rightarrow V = \dfrac{{2\sigma \pi }}{{4\pi {\varepsilon _0}}}\left[ {\sqrt {{r^2} + {x^2}} } \right]_0^R$
$\Rightarrow V = \dfrac{{2\sigma \pi }}{{4\pi {\varepsilon _0}}}\left[ {\sqrt {{R^2} + {x^2}} - \sqrt {{{\left( 0 \right)}^2} + {x^2}} } \right]$
$\Rightarrow V = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\sqrt {{R^2} + {x^2}} - x} \right]$
We know that the magnitude of the electric field at any point is given by the following equation
$E = - \dfrac{{dV}}{{dx}}$
So, the magnitude of the electric field at point P due to a uniformly charged disc is
$\Rightarrow E = - \dfrac{{d\left( {\dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\sqrt {{R^2} + {x^2}} - x} \right]} \right)}}{{dx}}$
$\Rightarrow E = - \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\dfrac{{d\left[ {\sqrt {{R^2} + {x^2}} } \right]}}{{dx}} - \dfrac{{dx}}{{dx}}} \right]$
$\Rightarrow E = - \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\dfrac{{2x}}{{2\sqrt {{R^2} + {x^2}} }} - 1} \right]$
$\Rightarrow E = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \dfrac{x}{{\sqrt {{R^2} + {x^2}} }}} \right]$

Note:
By the equation for electric potential and the magnitude of the electric field, i.e. $V = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\sqrt {{R^2} + {x^2}} - x} \right]$ and $E = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \dfrac{x}{{\sqrt {{R^2} + {x^2}} }}} \right]$ for the charged disc, that the electric potential is smallest near the disc and the magnitude of the electric field is maximum near the center.