Question

Find the electric field intensity at a point $P$ which is at a distance $R$ (point lying on the perpendicular drawn to the wire at one of its ends) from a semi-infinite uniformly charged wire. (linear charge density$= \lambda$ )

Answer 1

Hint The electric field intensity at a distance from the current element will be directly proportional to the charge and it will be inversely proportional to the square of the distance of separation of the charge and the semi-infinite uniformly charged wire. Write the $x$ component and the $y$ component of the electric field vector and integrate it for the elemental distance of uniformly charged wire and integrate.

Complete step by step answer
Let us draw a diagram as follows:

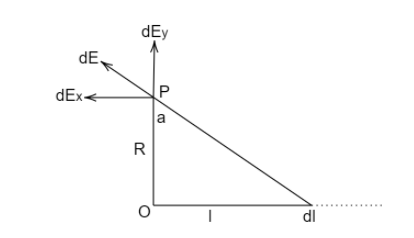
The electric field at the point $P$ due to a current element $dl$ in the uniform wire of linear charge density $\lambda$ can be split into two perpendicular components in the $x$ and $y$ directions. The electric field makes an angle $a$ at $P$ .
The charge $dq$ for an elemental length is given by
$dq = \lambda dl$
Using Pythagoras theorem, we get that the distance from the elemental length to the point $P$ is given as $\sqrt {{R^2} + {l^2}}$ .
The electric field due to the elemental length is given by
$dE = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{dq}}{{{R^2} + {l^2}}}$
Then we can write the $x$ component of the electric field as
$d{E_x} = - \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{\cos a}}{{{R^2} + {l^2}}}dq$
And we can write the $y$ component of the electric field as
$d{E_y} = - \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{\sin a}}{{{R^2} + {l^2}}}dq$
From the triangle formed in the figure, we get
$\cos a = \dfrac{R}{{\sqrt {{R^2} + {l^2}} }}$
And
$\sin a = \dfrac{l}{{\sqrt {{R^2} + {l^2}} }}$
Substituting these values and substituting for $dq$ as $\lambda dl$ in the equation for the $x$ and $y$ components of the electric field gives us
$d{E_x} = - \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{\lambda Rdl}}{{{{\left( {{R^2} + {l^2}} \right)}^{\dfrac{3}{2}}}}}$
$d{E_y} = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{\lambda ldl}}{{{{\left( {{R^2} + {l^2}} \right)}^{\dfrac{3}{2}}}}}$
Now integrating over the whole length will give us
${E_x} = \dfrac{1}{{4\pi {\varepsilon _o}}}\lambda R\int\limits_0^\infty {\dfrac{{dl}}{{{{\left( {{R^2} + {l^2}} \right)}^{\dfrac{3}{2}}}}}}$
Integrating this term will give us the $x$ component of the electric field as
${E_x} = \dfrac{{ - \lambda }}{{4\pi {\varepsilon _o}R}}$
And $y$ component can be computed as follows
${E_y} = \dfrac{1}{{4\pi {\varepsilon _o}}}\lambda \int\limits_0^\infty {\dfrac{{ldl}}{{{{\left( {{R^2} + {l^2}} \right)}^{\dfrac{3}{2}}}}}}$
Integrating the above term gives us
${E_y} = \dfrac{{ - \lambda }}{{4\pi {\varepsilon _o}R}}$
Therefore, the total electric field at the point $P$ will be
$E = \sqrt {{E_x}^2 + {E_y}^2}$
Substituting the values for ${E_x}$ and ${E_y}$, we get
$E = \sqrt {{{\left( {\dfrac{{ - \lambda }}{{4\pi {\varepsilon _o}R}}} \right)}^2} + {{\left( {\dfrac{{ - \lambda }}{{4\pi {\varepsilon _o}R}}} \right)}^2}}$
$\Rightarrow E = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{\sqrt 2 \lambda }}{R}$
As ${E_x} = {E_y}$ the angle $a = {45^ \circ }$.

Therefore, the electric field intensity at the point $P$ has a magnitude of $\dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{\sqrt 2 R}}{R}$ directed at an angle ${45^ \circ }$ .

Note
Note that in the question, it is mentioned that the wire is semi-infinite. This means that while taking the limits for integration, we have to take the limits from $0$ to $\infty$ and not from $- \infty$ to $+ \infty$ .
It is useful to use the vector components of any field or vectors when you come across such problems; where the vectors are inclined at an angle with respect to another given vector.