Question

Find the electric field at the center of an arc of linear charge density $\lambda$, radius R subtending angle $\phi$ at the center.

Answer 1

First of all consider small corresponding elements of arc on either side of the horizontal. Now find out the electric field produced due to them and the resolve and also cancel out the oppositely directed ones. Now substitute the standard expression for electric field due to charge density $\lambda$ and integrate over the length of the arc and thus get the required electric field.
Formula used:
Electric field,
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{R}^{2}}}$

Complete step-by-step solution
We are given an arc of linear charge density$\lambda$, that is, if Q is the total charge contained in the arc then,
$\lambda =\dfrac{Q}{R\phi }$
The arc is subtending angle $\phi$ at the center and the arc has a radius R. By symmetry we know that the electric field due to the arc will be radially outward at the center. To understand this, consider a small element of the arc of charge $dQ=\lambda Rd\theta$ on either side of horizontal to the arc.

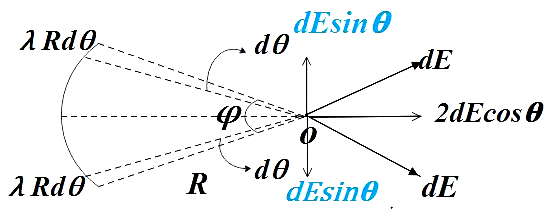
Now resolving the electric field due to small element of the arc$\lambda Rd\theta$, we see that both the vertical components get canceled and all that remains will be the horizontal component of the electric field due to the corresponding small elements.
So we have $2dE\cos \theta$ due to all such corresponding small elements on the arc, so, by integrating all those electric fields due to these small elements we get the electric field due to the whole arc.
$E=\int\limits_{0}^{\dfrac{\phi }{2}}{2dE\cos \theta }$ …………………………………….. (1)
We know that electric due to charge dQ is given by,
$dE=K\dfrac{dQ}{{{R}^{2}}}$
But, $dQ=\lambda Rd\theta$
$dE=K\dfrac{\lambda Rd\theta }{{{R}^{2}}}=K\dfrac{\lambda d\theta }{R}$ ……………………………… (2)
Substituting (2) in (3),
$E=\int\limits_{0}^{\dfrac{\phi }{2}}{2K\dfrac{\lambda \cos \theta d\theta }{R}}$
$\Rightarrow E=\dfrac{2K\lambda }{R}\int\limits_{0}^{\dfrac{\phi }{2}}{\cos \theta d\theta }$
$\Rightarrow E=\dfrac{2K\lambda }{R}\left[ \sin \theta \right]_{0}^{\dfrac{\phi }{2}}$
$\Rightarrow E=\dfrac{2K\lambda }{R}\left( \sin \left( \dfrac{\phi }{2} \right)-\sin 0 \right)$
$\Rightarrow E=\dfrac{2K\lambda \sin \dfrac{\phi }{2}}{R}$
Now substituting the value of K as $K=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$
$\therefore E=\dfrac{2\lambda }{4\pi {{\varepsilon }_{0}}R}\sin \dfrac{\phi }{2}$
Hence, we find the electric field at the centre of an arc of linear charge density$\lambda$, radius R subtending angle $\phi$ at the centre as,
$E=\dfrac{2\lambda }{4\pi {{\varepsilon }_{0}}R}\sin \dfrac{\phi }{2}$

Note: If the given arc subtended $\theta =180{}^\circ$ at its centre, that is, for a semicircle, we could substitute for $\phi$ to get the electric field due semicircle of charge density $\lambda$ as,
$E=\dfrac{2\lambda }{4\pi {{\varepsilon }_{0}}R}$
Similarly, you could find the electric field for any arc by substituting the subtended angle. For a full circle, we see that,
$E=\dfrac{2\lambda }{4\pi {{\varepsilon }_{0}}R}\sin \dfrac{360}{2}=\dfrac{2\lambda }{4\pi {{\varepsilon }_{0}}R}\left( 0 \right)=0$