Question
Question: Find the electric field at point P 
Solution
To solve these type of problem we need to take a very small portion of length and by calculating electric field due to this small portion on point P we will integrate over θ to calculate our required electric field at point P due to an electric charged arc.
Formula used:
Electric field due to a point charge,
⇒E=4π∈∘1R2Q
Complete answer:
From the above diagram we can observe that both half are equal and will exerts same amount of electric field on point P so, we just need to calculate field due to one half and by doing it’s two times we can get our required field at point P
Now, by taking a small section of charge dq in small angle dθ from point P on upper half and the charge per unit length is given as λso,
⇒dq=λRdθ and electric field due to this small portion will be dE at point P, by taking in electric field from both half into consideration and its component along x axis(y axis component will be cancelled) we have,
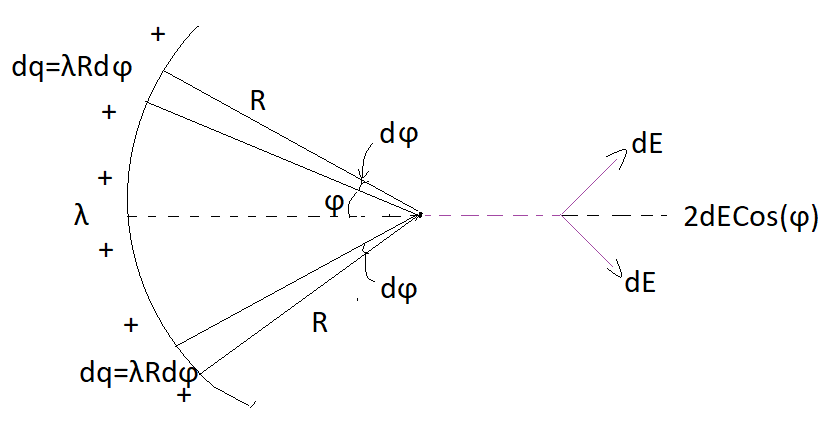
⇒dE=4π∈∘1R2λRdϕ
⇒dE=4π∈∘1Rλdϕ
Now, net field due to symmetric halfs at point P will be,
⇒dE=2dEcos(ϕ), now integrating this equation over 0 to 2θ ,
⇒E=∫dE=0∫2θ2dEcos(ϕ).dϕ
⇒E=0∫2θ24π∈∘1Rλcos(ϕ).dϕ
⇒E=24π∈∘1Rλ[sin(ϕ)]2θ 0
⇒E=4π∈∘1R2λsin(2θ)
∴ the electric field experienced by point P due to an uniformly charged arc will be given by,
⇒E=4π∈∘1R2λsin(2θ)
Note:
In the above problem we are considering a small portion of arc as a point particle and applying formula for electric field by a point particle. This is the standard procedure to calculate electric field at some point due to a uniformly charged body at some distance from it.
