Question
Question: Find the effective resistance between the points A and B in figure: 
Solution
In order to calculate the effective resistance between A and B, we must be aware to calculate the effective resistance in series and parallel combination. There are many closed circuits around AB such as ACB, ADCB, AEDCB and AFEDCB. So, we need to combine all these resistances and find the resultant of all of them.
Complete step by step solution:
The effective resistance for series combination is given as:
Rs=R1+R2+...+Rn
Where Rs is the resultant resistance for series combination and
R1,R2,Rn are the individual resistances.
Now, the resultant resistance for parallel combination is given as:
Rp1=R11+R21+...+Rn1
Where, Rp is the resultant resistance for parallel combination.
Now, from the diagram it is clear that the resistors between AF and FE are connected in series. Hence, the effective resistance between them will be 3Ω+3Ω=6Ω .
Now, this 6Ω resistance will be in parallel with the 6Ω resistance between AE as:
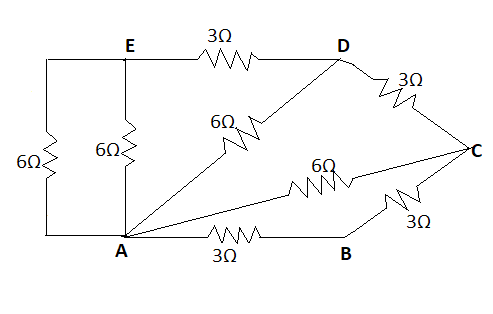
RAE1=61+61
⇒RAE=3Ω
Now, the diagram will be as follows:
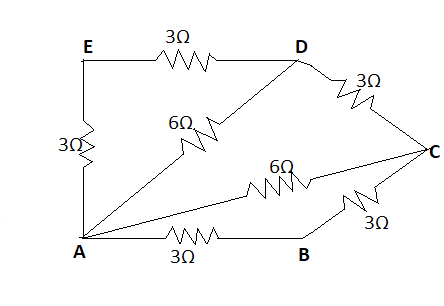
Now, resistors between AE and ED are in series, therefore the resultant will be given as:
RAD=3Ω+3Ω
⇒RAD=6Ω
Now, this RAD=6Ω will be in parallel with the middle resistor which has resistance of 6Ω. The resultant between AD will be given by parallel combination as
RAD1=61+61
⇒RAD=3Ω
The updated diagram will be as follows:
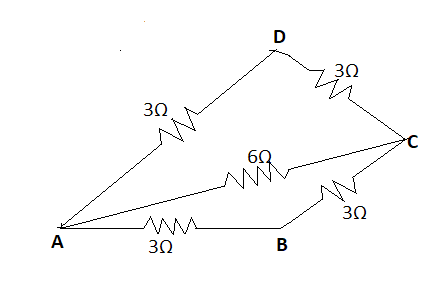
Now, we have resistances between AD and DC in series. Hence, the resultant of them will be:
3Ω+3Ω=6Ω and this 6Ω is parallel to the 6Ω resistance in the center of figure.
Now, we have 6Ω and 6Ω resistances which are in parallel between AC, their resultant will be:
RAC1=61+61
⇒RAC=3Ω
So, the updated diagram will be as follows:

As we have to find the resistance between A and B, hence we will consider AC and CB in series which will be in parallel to lower AB:
So for AC and CB in series the resultant resistance is given as:
RAB=3Ω+3Ω
⇒RAB=6Ω
This will be in parallel to lower AB hence the resultant will be:
RAB1=61+31
RAB=918
⇒RAB=2Ω
Therefore, the effective resistance between AB is 2Ω.
Note: We have to always remember that the effective resistance for series combination is given as:
Rs=R1+R2+...+Rn
And the effective resistance for parallel combination is given as:
Rp1=R11+R21+...+Rn1
This problem can be solved easily if diagrams are drawn after calculating effective resistance between two points.
