Question

Find the effective resistance between A and B

(A) $0.75\Omega$
(B) $10\Omega$
(C) $\dfrac{8}{7}\Omega$
(D) $\dfrac{6}{5}\Omega$

Answer 1

Hint
To find the equivalent resistance in the circuit given between the points A and B we need to use the formulas for the resistances in series and parallel circuits. On calculating step by step we get the equivalent resistance.

Formula Used: In this solution, we are going to use the following formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
And $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.

Complete step by step answer
Let us first draw the circuit by giving names to the different junctions in the circuit as,

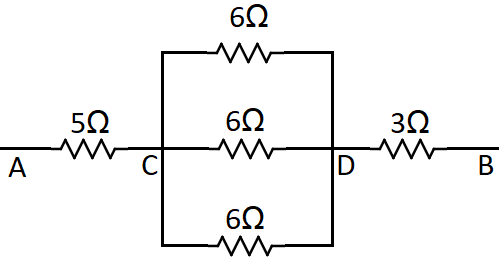
Now in between the points C and D we can see that there are 3 resistances which are placed parallel to each other. Now we can use the formula, $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$
Now in between points C and D there are 3 resistances $6\Omega$ each. So we can write,
${R_1} = {R_2} = {R_3} = 6\Omega$. Hence on substituting the values of the resistances in the formula we get,
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6}$
So taking the LCM as 6, we get
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{{1 + 1 + 1}}{6}$
Now taking the reciprocal, we get
${R_{eq1}} = \dfrac{6}{3}$
Cancelling the numerator and the denominator,
${R_{eq1}} = 2\Omega$
Now between A and B there are 3 resistances which are in series. So now will be using the formula, ${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$
The values are, ${R_1} = 5\Omega$, ${R_2} = {R_{eq1}} = 2\Omega$ and ${R_3} = 3\Omega$. Substituting the values we get,
${R_{eq}} = 5 + 2 + 3$
On adding we get,
${R_{eq}} = 10\Omega$
Hence the correct option will be option B.

Note
For the resistances which are in series, the current that is flowing through them will be the same. But for the resistances in parallel, the voltage across them will be equal and the current will depend on the value of the resistance.