Question

Find the effective resistance between A and B .

A. 1$\Omega$
B. 2$\Omega$
C. 3$\Omega$
D. 9$\Omega$

Answer 1

Hint: In series connection, equivalent resistance is the sum of the resistances and in parallel connection, reciprocal of equivalent resistance is the sum of the reciprocals of the resistances.

Complete step by step answer:
Resistance of a wire or resistor is the ability of the wire to resist the flow of current through it if there is a potential difference across it. When the resistors are connected in series, the equivalent resistance of that connection is the sum of the individual resistances.
i.e. ${{R}_{eff}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+{{R}_{4}}+.........+{{R}_{n}}$(where n is the number of resistors in the connection)
When the resistors are connected in parallel, the reciprocal of the effective resistance of that connection is the sum of the reciprocals of the individual resistances.
i.e. $\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+\dfrac{1}{{{R}_{4}}}+.......+\dfrac{1}{{{R}_{n}}}$ (where n is the number of resistors in the connection).
Now with these basics we will be able to solve the given question. When we look at the given circuit diagram, we can notice that in two of the parallel connections, the resistances $2\Omega$ and $1\Omega$ are in series. Always remember to check for the series connections first because the effective resistance of series connection is easier to calculate (since we just have to add them algebraically). Therefore, the effective resistance of this sections will be $2\Omega +1\Omega =3\Omega$
Now, the simplified circuit will look like:

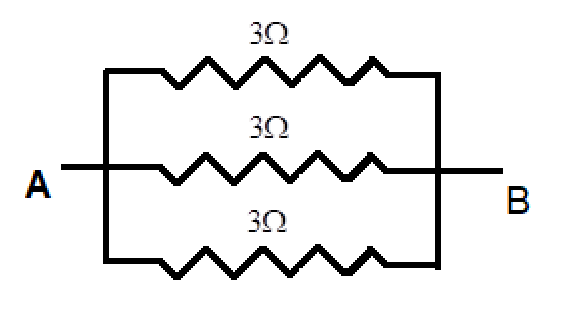
We can see that all the $3\Omega$ resistors are in parallel connection. Therefore,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}=\dfrac{3}{3}=1$
$\Rightarrow {{R}_{eff}}=1\Omega$
This means that instead of using all the resistors in the connections we can just connect a resistor of $9\Omega$.
Hence, the correct option is (a) $1\Omega$.

Note: Always keep in mind that when the resistors are connected in series, the same amount of current flows through all the resistors in the series connection. When the resistors are in parallel connection, they have the same potential difference across them.