Solveeit Logo
Login

Question

Question: Find the eccentricity of the ellipse \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\) whe...

Find the eccentricity of the ellipse x2a2+y2b2=1\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 where B is an end point of a minor axis, S and S’ are foci such that △BSS′\vartriangle BSS' is an equilateral triangle.

Explanation

Solution

Ellipse of the form x2a2+y2b2=1\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 is the one with semi major axis of length a parallel to x axis and semi minor with length b parallel to y axis. Eccentricity of an ellipse is the ratio of the distance between the centre and each focus of the ellipse to the semi major axis of the ellipse. That is e=cae = \dfrac{c}{a} . Or we have another formula to find the eccentricity e, e2=1−b2a2{e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}

Complete step-by-step answer:
Step 1: Let us represent the given data as a picture:

Step 2: Given that S and S’ are foci and B is the end point of the minor axis such that BSS’ forms an equilateral triangle. Thus our image will be,

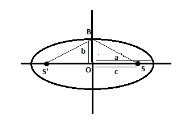
For an ellipse x2a2+y2b2=1\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1, with semi minor axis length a and eccentricity e, the focus S=(ae,0) and S’=(-ae,0) and B=(0,b). As the triangle is equilateral, all three sides will be equal. Thus,
SS’=S’B implies (SS′)2=(S′B)2{(SS')^2} = {(S'B)^2} … Formula1
where SS’ is the distance between the foci which is ae+ae=2ae and applying Pythagoras theorem in the triangle OBS’, square of hypotenuse = sum of squares of base and altitude implies,
(S′B)2=(OS′)2+(OB)2 =(ae)2+b2  {(S'B)^2} = {(OS')^2} + {(OB)^2} \\\ = {(ae)^2} + {b^2} \\\
Thus formula1 will be reframed as, (2ae)2=(ae)2+b2{(2ae)^2} = {(ae)^2} + {b^2}
Step 3: Simplifying the above we get,
4(ae)2−(ae)2=b2 3a2e2=b2  4{(ae)^2} - {(ae)^2} = {b^2} \\\ 3{a^2}{e^2} = {b^2} \\\
As we need the eccentricity e, we solve with respect to e.
3e2=b2a23{e^2} = \dfrac{{{b^2}}}{{{a^2}}} … Formula2
Step 4: Recalling the formula for eccentricity of an ellipse x2a2+y2b2=1\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1,
e2=1−b2a2{e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}… Formula 3
Substituting Formula 2 in Formula 3 we get, e2=1−3e2{e^2} = 1 - 3{e^2}
Implies
4e2=1 e=14  4{e^2} = 1 \\\ e = \sqrt {\dfrac{1}{4}} \\\
e=12e = \dfrac{1}{2}

Final Answer: Eccentricity , e=12e = \dfrac{1}{2}

Note: Other form of ellipse is x2b2+y2a2=1\dfrac{{{x^2}}}{{{b^2}}} + \dfrac{{{y^2}}}{{{a^2}}} = 1with the major axis along y axis and minor along x axis. Its foci will be (0, ae) and (0, -ae). Thus in general, the ellipse centred at (h, k) can be represented by the formula(x−h)2a2+(y−k)2b2=1\dfrac{{{{(x - h)}^2}}}{{{a^2}}} + \dfrac{{{{(y - k)}^2}}}{{{b^2}}} = 1 or vise versa according to the axis where the ellipse is oriented.