Question

Find the domain of $y={{\log }_{2}}x$ ?

Answer 1

The domain of a function is the set of its possible inputs where for which the function is defined. We should remember that the base of a logarithm must be a positive number and it should not be equal to 1. The base of $y={{\log }_{2}}x$ is x. So, x should be greater than 0 and should be equal to 1.

Complete step-by-step solution:
Before solving question we should know that the logarithmic function$y={{\log }_{b}}a$ is defined to be equivalent to the exponential equation $a={{b}^{y}}$ under the conditions $a>0,b>0,a\ne 1,b\ne 1$. We know that the domain of a function is the set of all possible inputs given to a function where the function is defined. The range is said to be defined as all the possible values obtained from the domain of the function.
From the question, we are given a function $y={{\log }_{2}}x$.
By comparing the function $y={{\log }_{2}}x$ with$y={{\log }_{b}}a$ , we get $a=x,b=2$.

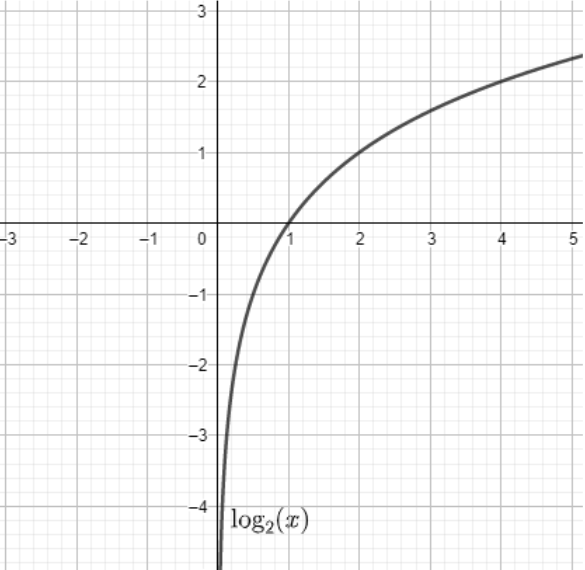
We know that for a logarithm $y={{\log }_{b}}a$ the following conditions are needed to be followed:

& 1)a>0 \\\ & 2)a\ne 1 \\\ & 3)b>0 \\\ & 4)b\ne 1 \\\ \end{aligned}$$ As the value of $$b=2$$, condition (3) and condition (4) are satisfied. The value of $$a=x$$, so to get condition (1) and condition (2) satisfied. The value of x should be greater than 1 and equal to zero. $$x>0,x\ne 1$$. So, the domain the function $$y={{\log }_{2}}x$$ is $$(0,1)\cup (1,\infty )$$. **Note:** There is an alternative method to solve this problem. We know that the logarithmic function $$y={{\log }_{b}}a$$ is defined to be equivalent to the exponential equation $$a={{b}^{y}}$$ under the conditions $$a>0,b>0,a\ne 1,b\ne 1$$. In the similar manner, we will write $$y={{\log }_{2}}x$$ as $${{2}^{y}}=x$$. Now, applying the condition on $${{2}^{y}}=x$$ from the conditions that we have shown for $$a={{b}^{y}}$$. 2 is already greater than 0 and x must be greater than 0. $x>0$ ……… (1) Also 2 and x must not be equal to 1. As it is clear that 2 is not equal to 1 and also x must not be equal to 1. $x\ne 1$ ………… (2) Combining (1) and (2) we get, $$x\in (0,1)\cup (1,\infty )$$ So, the domain the function $$y={{\log }_{2}}x$$ is: $$(0,1)\cup (1,\infty )$$