Question

Find the domain of the following function f\left( x \right)={{\log }_{4}}\left[ {{\log }_{5}}\left\\{ {{\log }_{3}}\left( 18x-{{x}^{2}}-77 \right) \right\\} \right].
(a) (7, 11)
(b) (8, 10)
(c) (-7, 11)
(d) (-8, 10)

Answer 1

First, before proceeding for this, we must know the following fact for the logarithm function that the domain of the log function is always greater than zero. Then, we should assume all the following brackets as a, b and c as $18x-{{x}^{2}}-77$ be a, ${{\log }_{3}}\left( 18x-{{x}^{2}}-77 \right)$ be b and {{\log }_{5}}\left\\{ {{\log }_{3}}\left( 18x-{{x}^{2}}-77 \right) \right\\} be c. Then, by applying the condition for the domain of log function in the above assumed variables a, b and c, we get the final domain.

Complete step-by-step answer :
In this question, we are supposed to find the domain of the following function f\left( x \right)={{\log }_{4}}\left[ {{\log }_{5}}\left\\{ {{\log }_{3}}\left( 18x-{{x}^{2}}-77 \right) \right\\} \right].
So, before proceeding for this, we must know the following fact for the logarithm function that the domain of the log function is always greater than zero.
So, the domain of log x is x > 0.
Now, we should assume all the following brackets as a, b and c:
So, let $18x-{{x}^{2}}-77$ be a.
Similarly, let ${{\log }_{3}}\left( 18x-{{x}^{2}}-77 \right)$ be b.
Also, let {{\log }_{5}}\left\\{ {{\log }_{3}}\left( 18x-{{x}^{2}}-77 \right) \right\\} be c.
Now, by applying the condition for the domain of log function in the above assumed variables a, b and c.
Then, firstly applying it for the variable a as:
$\begin{aligned} & a>0 \\\ & \Rightarrow 18x-{{x}^{2}}-77>0 \\\ & \Rightarrow \left( x-7 \right)\left( x-11 \right)<0 \\\ & \Rightarrow x\in \left( 7,11 \right) \\\ \end{aligned}$
Here, from the above condition we get x belongs to the range (7, 11) as:

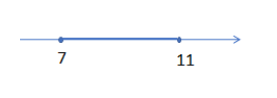
Now, by applying the same condition for variable b as:
$\begin{aligned} & b>0 \\\ & \Rightarrow {{\log }_{3}}\left( a \right)>0 \\\ & \Rightarrow a>{{3}^{0}} \\\ & \Rightarrow a>1 \\\ & \Rightarrow 18x-{{x}^{2}}-77>1 \\\ & \Rightarrow 18x-{{x}^{2}}-78>0 \\\ & \Rightarrow \left( -9-\sqrt{3}-x \right)\left( -9+\sqrt{3}+x \right)>0 \\\ & \Rightarrow x\in \left( 9-\sqrt{3},9+\sqrt{3} \right) \\\ \end{aligned}$
Here, from the above condition we get x belongs to the range $\left( 9-\sqrt{3},9+\sqrt{3} \right)$ as:

Now, by applying the same condition for variable c as:
$\begin{aligned} & c>0 \\\ & \Rightarrow {{\log }_{5}}\left( b \right)>0 \\\ & \Rightarrow b>{{5}^{0}} \\\ & \Rightarrow b>1 \\\ & \Rightarrow {{\log }_{3}}\left( a \right)>1 \\\ & \Rightarrow a>{{3}^{1}} \\\ & \Rightarrow a>3 \\\ & \Rightarrow 18x-{{x}^{2}}-77>3 \\\ & \Rightarrow 18x-{{x}^{2}}-80>0 \\\ & \Rightarrow \left( 8-x \right)\left( 10-x \right)>0 \\\ & \Rightarrow x\in \left( 8,10 \right) \\\ \end{aligned}$
Here, from the above condition we get x belongs to the range (8, 10) as:

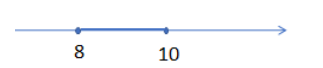
So, the domain must satisfy every condition and finally we get the domain as (8, 10).
Hence, option (b) is correct.

Note : Now, to solve these types of the questions we need to know some of the basic rules of the log function so that these questions are done easily and accurately. So, the basic rules of the log function are:
domain of log x is only valid for x>0.
Value of Log1=0.