Question

Find the domain of the following expression: $\sqrt{\dfrac{\left( 2\left| x \right|-4 \right)}{6}}$

Answer 1

To find the domain of the given expression we will start by solving the expression for $x$ and since it involves the absolute value of $x$and when we solve we will start first by taking $x$ as positive and then $x$ as negative and finally we will get two intervals for this expression which will be our domain.

Complete step-by-step answer :
We are given the expression: $\sqrt{\dfrac{\left( 2\left| x \right|-4 \right)}{6}}$ and we have to find the domain of it which means that we have to find out the values of $x$ which defines the expression.
Now, we know that the value of a square root is always equal to $0$ or greater than $0$.
Therefore, $\dfrac{2\left| x \right|-4}{6}\ge 0$ .
Now we will solve for $x$ :
So, to find the interval for the first piece that is when the inside of the absolute value is non-negative that is $x\ge 0$ , therefore: $\dfrac{2x-4}{6}\ge 0$ and to find out the interval for the second piece that is when the inside of the absolute value is negative that is for $x<0$ , therefore: $\dfrac{2\left( -x \right)-4}{6}\ge 0$ :
We will write it as piecewise:
\left\\{ \begin{matrix} & \dfrac{2x-4}{6}\ge 0\text{ }x\ge 0 \\\ & \dfrac{2\left( -x \right)-4}{6}\ge 0\text{ }x<0 \\\ \end{matrix} \right\\}\Rightarrow \left\\{ \begin{matrix} & \dfrac{x-2}{3}\ge 0\text{ }x\ge 0 \\\ & \dfrac{-x-2}{3}\ge 0\text{ }x<0 \\\ \end{matrix} \right\\}
Now, we will solve $\dfrac{x-2}{3}\ge 0$ for $x$ , now we will multiply both sides by $3$ :
$\dfrac{\left( x-2 \right).3}{3}\ge 0.3\Rightarrow \left( x-2 \right)\ge 0$ , we will take 2 on the right hand side, therefore: $x\ge 2$
Now all the values of $x$ will be defined for $x\ge 2$ ......... Equation 1.
Now, we will solve $\dfrac{-x-2}{3}\ge 0$ for $x$ , now we will multiply both sides by $3$ :
$\dfrac{\left( -x-2 \right).3}{3}\ge 0.3\Rightarrow \left( -x-2 \right)\ge 0$ , we will take -2 on the right hand side,
Therefore: $-x\ge 2\Rightarrow x\le -2$
Now all the values of $x$ will be defined for $x\le -2$ ......... Equation 2.
Now we will find the union of the solutions from equation 1 and equation 2: $\left( x\le -2 \right)\bigcup \left( x\ge 2 \right)$
Therefore the domain is all values of $x$ that makes the expression defined that is :
$\left( -\infty ,-2 \right]\bigcup \left[ 2,\infty \right)$

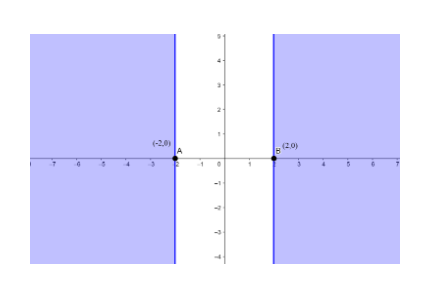
Note : Sometimes students can get confused between domain and range. Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.