Question

Find the domain of definition of the following function:
$y=\log \left( 5{{x}^{2}}-8x-4 \right)+{{\left( x+3 \right)}^{-0.5}}$

Answer 1

Start by finding the domain of the logarithmic part of the expression. We know that the term inside the log must be greater than 0, so use this to get the values of x which are possible for the logarithmic term to exist. Next move to the domain of ${{\left( x+3 \right)}^{-0.5}}$ , which can be written as $\dfrac{1}{\sqrt{x+3}}$ . As we know that the denominator cannot be negative and the part inside the root is always positive, we get x>-3. Take the intersection of the domains of the two terms to get the answer.

Complete step-by-step answer :
Let us start the solution to the above question by finding the domain of the logarithmic part first. The expression given to us is:
$y=\log \left( 5{{x}^{2}}-8x-4 \right)+{{\left( x+3 \right)}^{-0.5}}$
Now, let us first focus on $\log \left( 5{{x}^{2}}-8x-4 \right)$ . We know that the part inside the log must be greater than 0, as the log is defined only for positive real numbers.
$\therefore 5{{x}^{2}}-8x-4>0$
We know that we can write 8x as (10x-2x). On doing so, our inequality becomes:
$5{{x}^{2}}-\left( 10x-2x \right)-4>0$
$\Rightarrow 5{{x}^{2}}-10x+2x-4>0$
$\Rightarrow 5x\left( x-2 \right)+2\left( x-2 \right)>0$
$\Rightarrow \left( 5x+2 \right)\left( x-2 \right)>0$
So, the points where the LHS of the inequality is zero is x=2 and $x=-\dfrac{2}{5}$ . So, let us draw a number line and represent this:

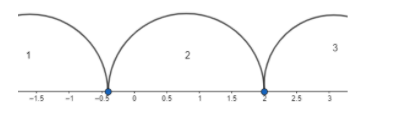
When the values of x are in region 1 or region 3, the inequality is satisfied, so the values of x satisfying the inequality are:
$x\in \left( -\infty ,-\dfrac{2}{5} \right)\cup \left( 2,\infty \right)$
Now let us focus on ${{\left( x+3 \right)}^{-0.5}}$ , which can be written as $\dfrac{1}{\sqrt{x+3}}$ . As we know that the denominator cannot be negative and the part inside the root is always positive, we can say
$x+3>0$
$\Rightarrow x>-3$
This can be written as $x\in \left( -3,\infty \right)$ .
Now we will take intersection between the domains of both the parts of the expression to get the domain of the whole expression.
$\text{Domain of expression}=\left( \left( -\infty ,-\dfrac{2}{5} \right)\cup \left( 2,\infty \right) \right)\cap \left( -3,\infty \right)$
$\text{Domain of expression}=\left( -3,-\dfrac{2}{5} \right)\cup \left( 2,\infty \right)$

Note : Remember when you use a number line to solve an inequality, RHS of the inequality should be zero, LHS should have all the factors getting multiplied. Then the points where the LHS is zero is represented on the number line, and the LHS of the inequality is greater than and smaller than zero for alternate regions such that the first region from the right is always the region in which the LHS is positive.