Question

Find the domain and the range of the real function f defined by $f(x) = \left|{x - 1} \right|$

Answer 1

As we have given the function we’ll check the domain of the function by examining that at what values of x the function is defined and then for finding the range of a function we’ll first assume the function as a new variable let say y, now we’ll transform the equation in such a way that the equation will become y in terms of x and check for which value of y, x is defined and that set will be the range of the function.

Complete step by step solution: Given data: $f(x) = \left|{x - 1} \right|$
From the function i.e. $f(x) = \left|{x - 1} \right|$, we can see that the function is defined for all values of x i.e. if we substitute x with any value we will get the particular value of the function corresponding to that value of x.
Therefore we can say that the domain of the function will be $\mathbb{R}$
i.e. the domain of $f(x) = ( - \infty ,\infty )$
Now, let y=f(x)
$\Rightarrow y = \left|{x - 1} \right|$
Now, we know that a modulus function always gives results greater or equal to zero.
Therefore, we can say that $\left|{x - 1} \right| \geqslant 0$
$\Rightarrow y \geqslant 0$
Therefore, $y \in \left[0,\infty \right)$
The range of the function $f(x) = \left[ 0,\infty \right)$

Note: Note: We can also solve the same question using the graph, for that we’ll plot the graph of the function in the Cartesian plane and all the values of the x-axis will be the domain and all the values resulting in the y-axis will be the range of the function.

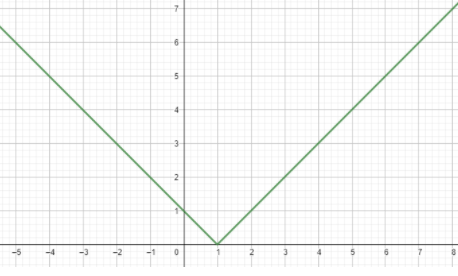
the domain of $f(x) = ( - \infty ,\infty )$
The range of the function $f(x) = \left[ 0, \infty \right)$