Question

Find the domain and range of the function $f\left( x \right) = {x^4} - 4{x^3} + 3{x^2}$ .

Answer 1

The relation between the set of possible inputs and the set of possible outputs where each input is related to exactly one output is called a function. The set of possible input values refers to a domain of the function and the set of possible output values refers to a range of the function.

Complete step by step answer:
In this problem, we have given a function $f\left( x \right) = {x^4} - 4{x^3} + 3{x^2}$ and, we know that domain is the set of all possible input values, so, in this function the domain becomes $- \infty$to $\infty$ , as in the function there is no denominator given then all the values from$- \infty$to$\infty$ are possible.
Now, to find the range,
$y = f\left( x \right) = {x^4} - 4{x^3} + 3{x^2}$
We have to find the values for$y$and when the value of $x$ becomes positive then the value of ${x^4}$ and$3{x^2}$ become more influential over$- 4{x^3}$ and if the value of $x$is less than$0$means negative, then the values of ${x^4}$ and$3{x^2}$remains positive and the value of $- 4{x^3}$also becomes positive as it has a odd power value and have a negative sign too. In this case, y grows faster. Now, we will find the values of $f\left( x \right)$ i.e, equal to$y$, by substituting the values of x.

$x$	$y = f\left( x \right) = {x^4} - 4{x^3} + 3{x^2}$
$- 1$	$8$
$0$	$0$
$1$	$0$
$2$	$- 4$
$3$	$0$

Now, let us graph the function,

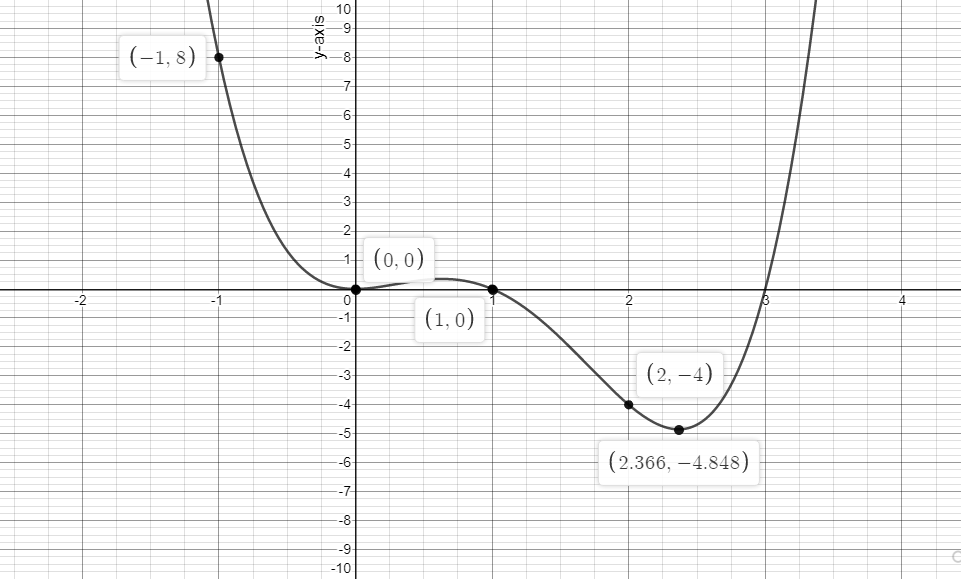
On graphing, we have found there is a point$\left( {2.366, - 4.848} \right)$, which is the lowest on the graph and as we know, range is the possible output values or $y$. So, the range of the function becomes $[ - 4.848,\infty )$.

Note: To find the domain of the function, we have to put the input values into the function so that the function will not become undefined and imaginary. Let us take an example, $\dfrac{1}{{1 - x}}$ , in this if we put$x = 1$ then the answer of the function become undefined, so, to find the domain of these type, we need to take $1 - x \ne 0$ then, we get $x \ne 1$, means the domain of this function will become less than $1$, more than $1$ but not equals to $1$.