Question

Find the domain and range of the following function:
$\begin{aligned} & \left( i \right)f\left( x \right)={{x}^{2}} \\\ & \left( ii \right)f\left( x \right)=\sqrt{\left( x-1 \right)\left( 3-x \right)} \\\ \end{aligned}$

Answer 1

To solve this question given above, we will first find out what the domain and range of a function is. Then, to find the domain of (i) and (ii), we will find out all the values of x for which $f\left( x \right)$ will exist. To find the range of (i), we will simply draw the graph of $y={{x}^{2}}$ and find all the values of y for which the graph exists. To find the range of (ii), we will differentiate the function given in (i) with respect to x. After that, we will analyze its derivative and on the basis of this, we will find its range.

Complete step-by-step answer:
Before we start solving this question, we will first find out what is the domain and range of a function. The domain of a function is defined as the set of all the values that the independent variable can take. The range of a function is the set of all the values the dependent variable can take. Now we will find the domain and range of (i) and (ii).
$\left( i \right)f\left( x \right)={{x}^{2}}$
We can see here that x can take any value and for any value of x, $f\left( x \right)$ is defined. Thus, the domain of $f\left( x \right)$ is $\left( -\infty ,\infty \right)$.
To find the range, we will draw the graph of $y={{x}^{2}}$.

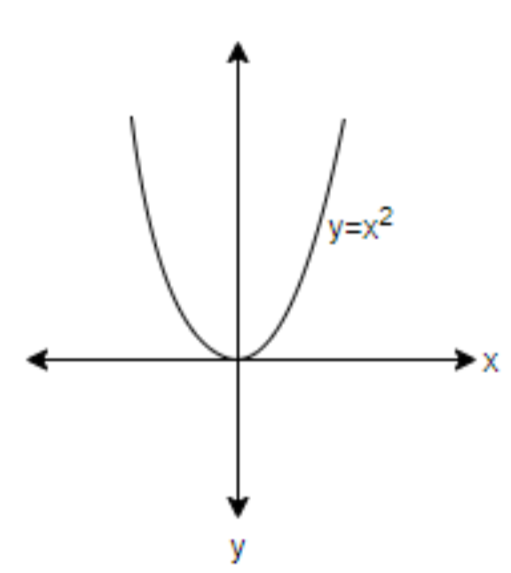
Here, the value of y is positive and zero only. So, the range will be $f\left( x \right)\in [0,\infty )$.
$\left( ii \right)f\left( x \right)=\sqrt{\left( x-1 \right)\left( 3-x \right)}$
Now, we can see that x cannot take nay value. It can take those values only where $\left( x-1 \right)\left( 3-x \right)$ is greater than or equal to zero. Thus :
$\begin{aligned} & \left( x-1 \right)\left( 3-x \right)\ge 0 \\\ & \left( x-1 \right)\left( x-3 \right)\le 0 \\\ \end{aligned}$

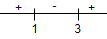
So, it implies $x\in \left[ 1,3 \right]$. Thus, the domain will be $x\in \left[ 1,3 \right]$.
Now, to find the range, we will find the derivative of $f\left( x \right)$. Thus, we have,
$\dfrac{df\left( x \right)}{dx}=\dfrac{d}{dx}\left[ \sqrt{\left( x-1 \right)\left( 3-x \right)} \right]$
Now, we know that according to the product rule, $\dfrac{d}{dx}\left( a.b \right)=b.\dfrac{da}{dx}+a.\dfrac{db}{dx}$. Thus, we have,
$f'\left( x \right)=\sqrt{3-x}\dfrac{d\left( \sqrt{x-1} \right)}{dx}+\sqrt{x-1}\dfrac{d\left( \sqrt{3-x} \right)}{dx}$
And we know that, $\dfrac{d\sqrt{ax+b}}{dx}=\dfrac{a}{2\sqrt{ax+b}}$. So, using this formula, we will get,
$\begin{aligned} & f'\left( x \right)=\dfrac{\sqrt{3-x}}{2\sqrt{x-1}}-\dfrac{\sqrt{x-1}}{2\sqrt{3-x}} \\\ & \Rightarrow f'\left( x \right)=\dfrac{\left( 3-x \right)-\left( x-1 \right)}{4\sqrt{\left( x-1 \right)\left( 3-x \right)}} \\\ & \Rightarrow f'\left( x \right)=\dfrac{4-2x}{4\sqrt{\left( 3-x \right)\left( x-1 \right)}} \\\ & \Rightarrow f'\left( x \right)=\dfrac{2-x}{2\sqrt{\left( 3-x \right)\left( x-1 \right)}} \\\ \end{aligned}$
Now, let’s plot the graph for this derivative:

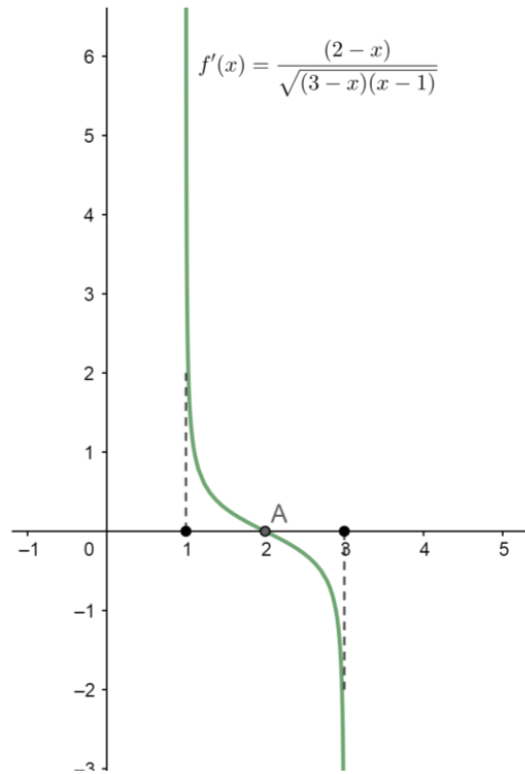
Here, we can see that $f'\left( x \right)>0$ in $\left( 1,2 \right)$ and $f'\left( x \right)<0$ in $\left( 2,3 \right)$. Thus, x = 2 will be the maxima. Thus the minimum of $f\left( x \right)$ will be when x =3 and x = 1 and it will be maximum when x = 2. Thus,
$\begin{aligned} & f\left( 3 \right)=f\left( 1 \right)=0 \\\ & f\left( 2 \right)=1 \\\ \end{aligned}$
Thus, the range of $f\left( x \right)$ is $f\left( x \right)\in \left[ 0,1 \right]$.

Note: We can also find the range of $f\left( x \right)={{x}^{2}}$ by the following method. We know that when the derivative of a function is zero, the value of x at which it is zero will be either maxima or minima. Thus, the derivative of $f\left( x \right)$ is,
$\dfrac{df\left( x \right)}{dx}=\dfrac{d}{dx}\left( {{x}^{2}} \right)=2x$
Now, $\dfrac{df\left( x \right)}{dx}=0$, so we have, $2x=0\Rightarrow x=0$. Now, x = 0 can’t be maxima as the maximum value of $f\left( x \right)={{x}^{2}}$ is infinity, but when we put x = 0 in $f\left( x \right)$, we will get $f\left( 0 \right)=0$. Thus, the range of $f\left( x \right)={{x}^{2}}$ is $f\left( x \right)\in [0,\infty )$.