Question

Find the domain and range of $tan ^{-1} x$ by plotting the graph.

Answer 1

In the simplest form domain is all the values that go into the function and range is all the functions that come out of it.

Complete step-by-step answer:
Let us define the domain and range of
y =tan x
The domain of the function y =tan x is
$x \in (-\dfrac{\pi}{2},\dfrac{\pi}{2})$
The range of the function y =tan x is
$y \in (-\infty , +\infty )$
The function $y= tan ^{-1} x$ is symmetric to the function y=tan x with respect the line y=x
Therefore, the domain is $x \in (-\infty , +\infty )$
and the range is $y \in (-\dfrac{\pi}{2},\dfrac{\pi}{2})$
Now we can draw the graph of the function from the observation and discuss it.

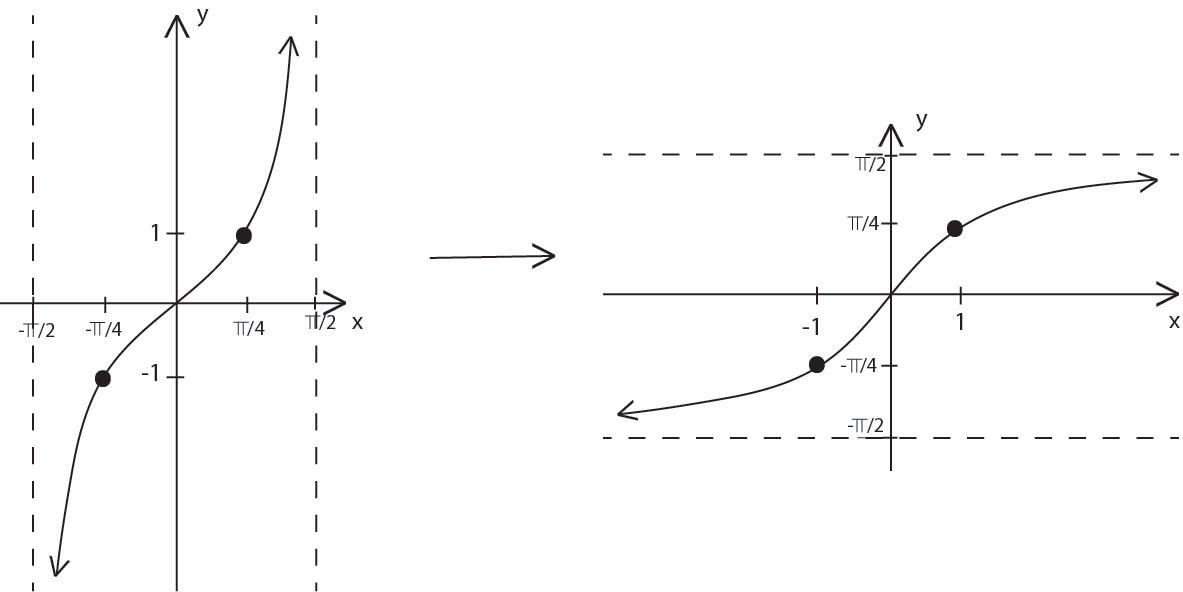
This the graph for the $y= tan ^{-1} x$ function.
Since the inverse function is obtained by reflecting the graph about the line y=x ,
The vertical asymptotes of the tangent function become horizontal asymptotes of the inverse tangent function.
As $\theta$ approaches $\infty , tan ^{-1} \theta$ approaches $-\dfrac{\pi}{2} \,as\, \theta \Rightarrow \theta , tan ^{-1} \theta \Rightarrow \dfrac{\pi}{2}$
And by reflecting the function we get the graph of the function.

Note: In the first step students need to take this assumption y= tan x otherwise they would not be able to solve the problem. Also the students need to clearly understand the meaning of domain and range of a function to solve the problem.