Question
Question: Find the distance between the point \(\left( 4,-2 \right)\) and \(\left( -5,1 \right)\) . A. 4.89...
Find the distance between the point (4,−2) and (−5,1) .
A. 4.897
B. 8.947
C. 7.149
D. 9.487
E. None of these
Solution
Hint: Use the distance formula between two points in the 2-D plane. It is given for two points (x1,y1) and (x2,y2) as (x1−x2)2+(y1−y2)2. Put values of coordinates given in the question in the above mentioned equation and get the answer. Use a division method to find the square root.
Complete step-by-step answer:
Here, we have two points (4,−2) and (−5,1) and need to determine the distance between them.
Now, we can use the distance formula for two points in 2-D geometry to calculate distance between the points. So, we can give distance formula between two points A and B whose coordinates on 2-D plane is given as (x1,y1) and (x2,y2) respectively as
AB=(x1−x2)2+(y1−y2)2 ...............................................(i)
We can represent the given points on 2-D plane as
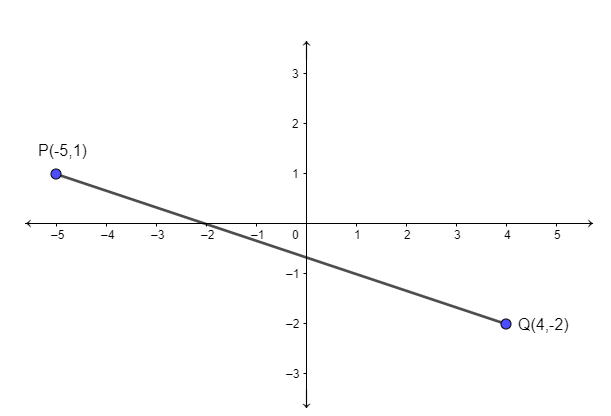
Now, we can put values of the given coordinates in the equation (i) and can suppose (x1,y1) as Q(4,−2) and (x2,y2) as P(−5,1). So, we get
Values of (x1,y1) and (x2,y2) as
x1=4 , x2=−5
y1=−2 , y2=1
Now, we can get length PQ as
PQ=(4−(−5))2+(−2−1)2
PQ=(4+5)2+(−3)2
⇒PQ=92+9
PQ=81+9=90 …………………………………………………..(ii)
Now, we can get the root of 90 in decimal form using the division method for finding the square root of 90.
So, we can put the bar to 90 and get 90. Now, we need to observe the least square number to 90.
92<90<102
81<90<102
So, we get
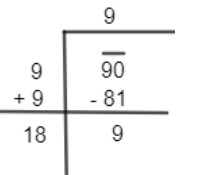
Now, we can observe that the square root of 90 will be in decimal form, so we can put 00 by putting a decimal after the given number i.e. 90, and put decimal after 9 in the quotient as well. So, we get
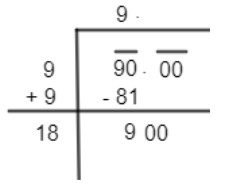
Now put a digit from 0 to 9 after 18 and same the decimal in quotient as well to get multiplication of it just less than 900.
So, we can observe that
185×5=925
185×4=736
So, we get
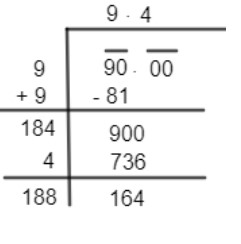
Now, we can put 00 again to get another digit after the decimal. So, similarly we get

So, we can get a square root of 90 with four digits after decimal as 9.4866.
Now, we can approximate it to the three digits after the decimal and can round off it till the third digit.
Hence, we get
90=9.487
So, the distance between two points (4,−2) and (5,−1) is 9.487.
Hence, option (D) is correct.
Note: One may get confused with the distance formula and can apply it as (x1−y1)2+(x2−y2)2, which is wrong. So, be careful with the formula for finding the distance between two points. One can take the orders of ( x1 and x2 ) and ( y1 and y2 ) in any order in the distance formula as (x1−x2)2 or (x2−x1)2 will give same value, similarly (y1−y2)2 and (y2−y1)2 will give same value as well. So, don’t get confused here.
It means distance formula can be given as
(x1−x2)2+(y1−y2)2
⇒(x2−x1)2+(y2−y1)2
90 can only be solved by using the division method for finding square roots, So, be careful with the division method as well because it involves decimals in its square root. Take .00 after decimal of 90 to get the digits of the square root after the decimal.
