Question

Find the distance between the parallel lines $3x+4y+7=0$ and $3x+4y-5=0$.

Answer 1

We first express the formula of distance as $d=\left| \dfrac{{{c}_{1}}-{{c}_{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ between two parallel lines $ax+by+{{c}_{1}}=0$ and $ax+by+{{c}_{2}}=0$. From the given equations of $3x+4y+7=0$ and $3x+4y-5=0$, we place the values in the formula to find the final solution.

Complete step by step solution:
We follow the formula for two parallel lines $ax+by+{{c}_{1}}=0$ and $ax+by+{{c}_{2}}=0$.
The distance between those lines will be $d=\left| \dfrac{{{c}_{1}}-{{c}_{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$.
We now find the distance between the parallel lines $3x+4y+7=0$ and $3x+4y-5=0$.
Equating with the general equation we get $a=3,b=4$.
The values of the constants are ${{c}_{1}}=7,{{c}_{2}}=-5$.
We put the values in the equation of $d=\left| \dfrac{{{c}_{1}}-{{c}_{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ to get $d=\left| \dfrac{7-\left( -5 \right)}{\sqrt{{{3}^{2}}+{{4}^{2}}}} \right|$.
Therefore, simplifying we get $d=\left| \dfrac{12}{\sqrt{25}} \right|=\dfrac{12}{5}=2.4$.
The distance between the parallel lines $3x+4y+7=0$ and $3x+4y-5=0$ is $2.4$ units.

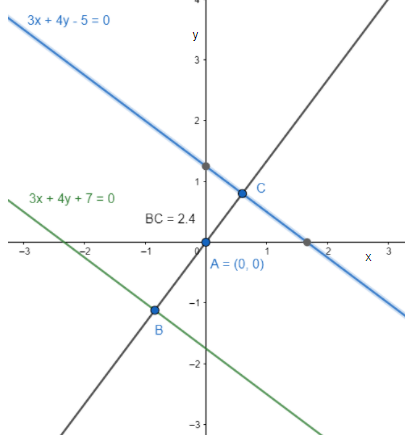
Note: The shortest distance between two parallel lines is the length of the perpendicular segment between them. It doesn't matter which perpendicular line we choose, as long as the two points are on the lines.