Question

Find the distance between the following pair of points: $\left( a,b \right);\left( c,b \right)$.

Answer 1

We first use the formula of distance between two points $\left( x,y \right)$ and $\left( m,n \right)$ as $d=\sqrt{{{\left( x-m \right)}^{2}}+{{\left( y-n \right)}^{2}}}$ for the general form. We then place the values for points $\left( a,b \right)$ and $\left( c,b \right)$ to find the approximate value of the distance.

Complete step by step answer:
We have to find the distance between points $\left( a,b \right)$ and $\left( c,b \right)$.
We first find the general formula for distance between two arbitrary points.
We take two points $\left( x,y \right)$ and $\left( m,n \right)$.
The formula for distance between those two points will be $d=\sqrt{{{\left( x-m \right)}^{2}}+{{\left( y-n \right)}^{2}}}$.
For our given points $\left( a,b \right)$ and $\left( c,b \right)$, we put the values for $x=a,y=b$ and $m=c,n=b$.
Therefore, the distance between those two points is $d=\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-b \right)}^{2}}}$.
Simplifying we get $d=\sqrt{{{\left( a-c \right)}^{2}}+0}=\sqrt{{{\left( a-c \right)}^{2}}}=\left| a-c \right|$ units.
Therefore, the distance between the following pair of points: $\left( a,b \right);\left( c,b \right)$ is $\left| a-c \right|$ units.

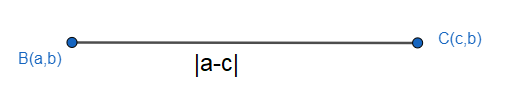
We take an actual example to simplify the explanation.
Let’s assume we have to find the distance between points $\left( -7,11 \right)$ and $\left( 8,11 \right)$.
For our given points $\left( -7,2 \right)$ and $\left( 11,-5 \right)$, we put the values for $a=-7,b=11$ and $c=8,b=11$.
Therefore, the distance between those two points is $d=\sqrt{{{\left( -7-8 \right)}^{2}}+{{\left( 11-11 \right)}^{2}}}=\sqrt{{{\left( -7-8 \right)}^{2}}}$
Simplifying we get $d=\left| -7-8 \right|=15$ units.

Note: We need to remember that when we are taking the modulus value because distance cannot be negative as it is a scalar value. The negative sign indicates the direction only. So, the modulus value changes it to its value to give the distance.